
如图15.1,已知抛物线C经过原点,对称轴x=-3与抛物线相交于第三象限的点M,与x轴相交于点N,且tan∠MON = 3.
(1)求抛物线C的解析式;
(2)将抛物线C绕原点O旋转180º得到抛物线C’,抛物线C’与x轴的另一交点为A,B为抛物线C’上横向坐标为2的点. www.12999.com
①若P为线段AB上一动点,PD⊥y轴于点D,求△APD面积的最大值;
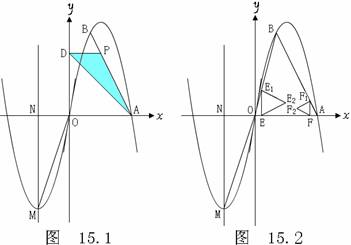 ②过线段OA上的两点E、F分别作x轴的垂线,交折线 O –B -A于点E1、F1,再分别以线段EE1、FF1为边作如图15.2所示的等边△EE1E2、等边△FF1F2,点E以每秒1个单位长度的速度从点O向点A运动,点F以每秒1个单位长度的速度从点A向点O运动,当△EE1E2有一边与△FF1F2的某一边在同一直线上时,求时间t的值.
②过线段OA上的两点E、F分别作x轴的垂线,交折线 O –B -A于点E1、F1,再分别以线段EE1、FF1为边作如图15.2所示的等边△EE1E2、等边△FF1F2,点E以每秒1个单位长度的速度从点O向点A运动,点F以每秒1个单位长度的速度从点A向点O运动,当△EE1E2有一边与△FF1F2的某一边在同一直线上时,求时间t的值.
解:(1)对称轴MN的解析式为x =-3, ON=3,tan∠MON = 3 ,MN=9,M(-3,-9),
令抛物线C的解析式为y=a(x+3)2-9,它经过原点,则0=a(0+3)2-9, a=1,
y=1(x+3)2-9=x2+6x ,所以抛物线C的解析式为y=x2+6x;
(2)①抛物线C’的解析式为
y=- x2+6x,当y=0时,x=0或6,点A的坐标为(6,0), 点B在抛物线C’上,且其横坐标为2,y=8,有点B(2,8),直线AB的解析式为
y=-2x +12 ,点P在线段AB上,令点P的坐标为(p,-2p+12),
S△APD = 12p(-2p+12)=- p2+6p =-(p-3)2+9,当p=3(2<3<8)时,
S△APD 的max值为9;
② 据(2)①知,直线OB解析式为y=4x,
直线AB解析式为y=-2x +12;
如图15.3, ∵EE1//FF1, △EE1E2、△FF1F2是等边三角形,∴E1E2//FF2,EE2//F1F2,
直线EE1的解析式为x=t,直线FF1的解析式为x=6-t,令E1 (t,y)则有E(t,0)、
E2 (t+ 32,y2),设直线EE2的解析式为
y=33x + a,直线F1F2的解析式为y= 33x + b,直线E1E2的解析式
为y=- 33x + c,直线FF2的解析式为y=- 33x + d,
Ⅰ、当EE1与FF1在同一直线上时,x=t=6-t,t=3 ;
Ⅱ、当0≤t≤2时,点E1在直线OB上,点F1在直线AB上,有E(t,0)、E1 (t,4t)、F (6-t,0)、F1(6-t,2t)
(a)当EE2与F1F2在同一直线上时,有0 = 33t + a,a=- 33t,
2t= 33(6-t) + b, b= (2+ 33)t-23, a=b, - 33t=(2+ 33)t-23,
t= 32;新 课 标 第 一 网
(b) 当E1E2与FF2在同一直线上时,有4t=- 33t + c,c=(4+ 33)t,
0=- 33(6-t) + d, d=23- 33t, c=d, (4+ 33)t = 2 3- 33t,
t= 311;
通过作图观察可知,当2<t≤6时,EE1与FF1不可能在同一直线上,E1E2与FF2也不可能在同一直线上。
综上所述,当△EE1E2有一边与△FF1F2的某一边在同一直线上时,t的值为3,32或 311.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
先找规律,再填数:
3-2=1
8+7-6-5=4
15+14+13-12-11-10=9
24+23+22+21-20-19-18-17=16
…………………
第100行的第一个数为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
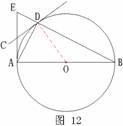
如图12,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.
(1) 求证:直线CD是⊙O的切线;
(2) 过点A作直线AB的垂线交BD的延长线于点E,且AB=5,BD=2,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
“红灯停,绿灯行”是我们在日常生活中必须遵守的交通规则,这样才能保
交通顺畅和行人安全。小刚每天从家骑自行车上学都经过三个路口,且每个路
只安装了红灯和绿灯,假如每个路口红灯和绿灯亮的时间相同,那么小刚从家
时出发去学校,他遇到两次红灯的概率是( )
A、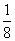 B、
B、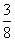 C、
C、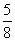 D、
D、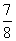
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com