
分析 根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2016除以4,根据商和余数的情况确定点A2016的坐标即可.
解答 解:∵点A1的坐标为(3,1),
∴A2(-1+1,3+1),
即(0,4),A3(-4+1,0+1),
即(-3,1),A4(1-1,-3+1),
即(0,-2),A5(3,1),
…,
依此类推,每4个点为一个循环组依次循环,
∵2016÷4=504,
∴点A2016的坐标与A4的坐标相同,为(0,-2);
故答案为:(0,-2).
点评 此题考查点的坐标规律,读懂题目信息,理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键.


科目:初中数学 来源: 题型:解答题
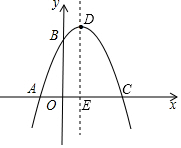 已知抛物线C1经过A(-1,0),B(0,3),C(3,0)三点,其顶点为点D,对称轴与x轴交于点E.
已知抛物线C1经过A(-1,0),B(0,3),C(3,0)三点,其顶点为点D,对称轴与x轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com