
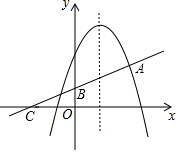
 ��ͼ������Ϊ��1��4����������y=ax2+bx+c��ֱ��y=$\frac{1}{2}$x+n���ڵ�A��2��2����ֱ��y=$\frac{1}{2}$x+n��y�ύ�ڵ�B��x�ύ�ڵ�C
��ͼ������Ϊ��1��4����������y=ax2+bx+c��ֱ��y=$\frac{1}{2}$x+n���ڵ�A��2��2����ֱ��y=$\frac{1}{2}$x+n��y�ύ�ڵ�B��x�ύ�ڵ�C���� ��1�����ô���ϵ���������n��ֵ��������������߽���ʽ��
��2�������öԳ����жϳ�MN=2NH�������������̻���õ�m=-2x2+4x�٣����жϳ���COB�ס�CMH�͡�HMP'�ס�CMH���жϳ�MH=2PN�������������̻���ó�4x=3m-2��������������⼴�ɣ�
��3����ABΪƽ���ı��εĶԽ��ߺͱ��ɵó���E�����꣮
��� �⣺��1��A��2��2������$y=\frac{1}{2}x+n$��n=1
�������ߵĽ���ʽy=a��x-1��2+4�����A��2��2�����ɵ�a=-2
���������ߵĽ���ʽy=2��x-1��2+4=-2x2+4x+2��
��2����ͼ1�� ��PP'��AC�Ľ���ΪH��
��PP'��AC�Ľ���ΪH��
��HM��x����M����PN��HM��N
��$P��x��-2{x^2}+4x+2����H��m��\frac{1}{2}m+1��$��
�ߵ�P'�ǵ�P����AC�ĶԳƵ㣬
��PH=P'H��
�ã���HNP�ա�HMP'��
��MH=NH��
��NM=2NH��
��-2x2+4x+2=m+2��
��m=-2x2+4x��
��ֱ��AC�Ľ���ʽΪy=$\frac{1}{2}$x+1��
��B��0��1����C��-2��0����
��OB=1��OC=2��
��OB��HM��
���COB�ס�CMH��
��$\frac{OC}{CM}=\frac{OB}{MH}$��
��CM=2MH��
��֤����HMP'�ס�CMH��
��$\frac{P'M}{MH}=\frac{MH}{CM}$��
��$\frac{P'M}{MH}=\frac{MH}{2MH}$=$\frac{1}{2}$��
��MH=2P'M=2PN
��$\frac{1}{2}m+1=2��m-x��$��
��4x=3m-2��
�����٢ڽ��x=1��$x=\frac{1}{3}$��
���P�����꣨1��4����$��\frac{1}{3}��\frac{28}{9}��$��
��3�����E����ΪA��t��0������ABΪ��Խ��߽��з������ۣ�
����ͼ4����AB��ƽ���ı��еı�ʱ��AB��DE��AB=DE
���ڵ�B��0��1��������ƽ��2����λ��������ƽ��1����λ�õ�A��2��2����
���D��������Ա�ʾΪD��t+2��1��
��D��t+2��1������y=2��x-1��2+4����-2��t+1��2+4=1
���$t=\frac{{-2��\sqrt{6}}}{2}$��
��ʱ$E��\frac{{-2+\sqrt{6}}}{2}��0��$��$��\frac{{-2-\sqrt{6}}}{2}��0��$��
�ڵ�AB��ƽ���ı��εĶԽ���ʱ��
��AB���е�$G��1��\frac{3}{2}��$����E��t��0����
����$G��1��\frac{3}{2}��$�ĶԳƵ�D��������Ա�ʾΪ��2-t��3��
��D��2-t��3������y=-2��x-1��2+4����-2��1-t��2+4=3
���$t=\frac{{-2��\sqrt{2}}}{2}$��
��$E��\frac{{-2+\sqrt{2}}}{2}��0��$��$��\frac{{-2-\sqrt{2}}}{2}��0��$��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ������ȫ�������ε��ж������ʣ����������ε��ж������ʣ�ƽ���ı��ε����ʣ��⣨2���Ĺؼ��ǵó�MN=2NH��MH=2PN���⣨3���Ĺؼ��Ƿ������ۣ��Ȿ����ص����÷��̵�˼��˼�����⣬��һ���ѶȱȽϴ���п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
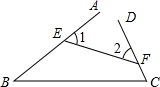 ��ͼ����E��F�ֱ���AB��CD�ϣ�����B=40�㣬��C=70�㣬���1+��2=110�㣮
��ͼ����E��F�ֱ���AB��CD�ϣ�����B=40�㣬��C=70�㣬���1+��2=110�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��-$\frac{2}{3}$ | B�� | a��2 | C�� | a��-$\frac{2}{3}$ | D�� | a��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
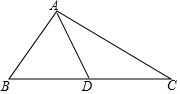 ��ͼ����ABC�У�AD�����ߣ���BAD=��B+��C��tan��ABC=$\frac{11}{10}$����tan��BAD=$\frac{33}{10}$��
��ͼ����ABC�У�AD�����ߣ���BAD=��B+��C��tan��ABC=$\frac{11}{10}$����tan��BAD=$\frac{33}{10}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
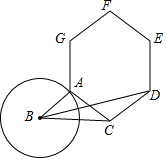 ��ͼ��BC=2��AΪ�뾶Ϊ1�ġ�B��һ�㣬����AC����AC�Ϸ���һ����������ACDEFG������BD����BD�����ֵΪ$2\sqrt{3}+1$��
��ͼ��BC=2��AΪ�뾶Ϊ1�ġ�B��һ�㣬����AC����AC�Ϸ���һ����������ACDEFG������BD����BD�����ֵΪ$2\sqrt{3}+1$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com