
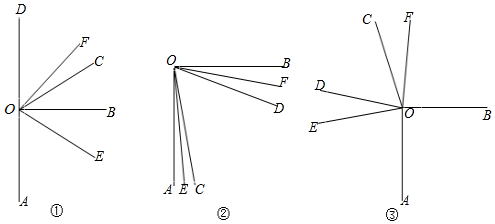
分析 (1)根据平角的定义可求∠AOC,∠BOD的度数,再根据角平分线的定义求得∠AOE,∠FOD的度数,再根据平角的定义可求∠EOF的度数;
(2)设∠AOE=∠COE=x,根据角的和差关系得到∠BOD=30°-2x,根据角平分线的定义得到∠BOF=15°-x,再∠EOF=∠AOB-(∠AOE+∠BOF)即可求解;
(3)设∠BOC=2x,则∠AOC=360°-∠AOB-∠BOC=270°-2x,∠BOD=∠BOC+∠COD=2x+60°,根据角平分线的定义得到∠COE=$\frac{1}{2}$∠AOC=135°-x,同理∠DOF=$\frac{1}{2}$∠BOD=x+30°,可得∠EOF=∠COE+∠DOF-∠COD=105°,再根据角平分线的定义得到∠EON的度数.
解答 解:(1)∵∠COD=60°,∠AOB=90°,
∴∠AOC=120°,∠BOD=90°,
∵OE平分∠AOC,OF平分∠BOD,
∴∠AOE=60°,∠FOD=45°,
∴∠EOF=180°-60°-45°=75°;
(2)∵OE平分∠AOC,
∴设∠AOE=∠COE=x,
∴∠BOD=∠AOB-∠AOC-∠COD=90°-2x-60°=30°-2x,
又∵OF平分∠BOD,
∴∠BOF=$\frac{1}{2}$∠BOD=$\frac{1}{2}$(30°-2x)=15°-x,
∴∠EOF=∠AOB-(∠AOE+∠BOF)=90°-(x+15°-x)=75°,
(3)设∠BOC=2x,
则∠AOC=360°-∠AOB-∠BOC=360°-90°-2x=270°-2x,
∠BOD=∠BOC+∠COD=2x+60°,
∵OE平分∠AOC,
∴∠COE=$\frac{1}{2}$∠AOC=135°-x,
同理∠DOF=$\frac{1}{2}$∠BOD=x+30°,
∴∠EOF=∠COE+∠DOF-∠COD=105°,
又∵ON平分∠EOF
∴∠EON=$\frac{1}{2}$∠EOF=52.5°.
故答案为:75°.
点评 本题考查的是角的计算,角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.


科目:初中数学 来源: 题型:填空题
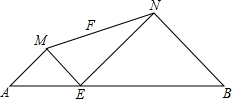 如图,已知AB=9,点E是线段AB上的动点,分别以AE、EB为底边在线段AB的同侧作等腰直角△AME和△BNE,连接MN,设MN的中点为F,当点E从点A运动到点B时,则点F移动路径的长是$\frac{9}{2}$.
如图,已知AB=9,点E是线段AB上的动点,分别以AE、EB为底边在线段AB的同侧作等腰直角△AME和△BNE,连接MN,设MN的中点为F,当点E从点A运动到点B时,则点F移动路径的长是$\frac{9}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
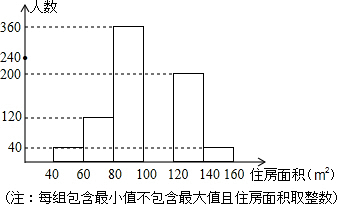 某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机的问卷调查,共发放1000份调查问卷,并全部收回,根据调查问卷,将消费者年收入的情况整理后,制成表格如下,将消费者打算购买住房面积的情况整理后,作出部频数分布直方图如图:
某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机的问卷调查,共发放1000份调查问卷,并全部收回,根据调查问卷,将消费者年收入的情况整理后,制成表格如下,将消费者打算购买住房面积的情况整理后,作出部频数分布直方图如图:| 年收入(万元) | 1.2 | 1.8 | 3.0 | 5.0 | 10.0 |
| 被调查的消费者数(人) | 200 | 300 | 400 | 70 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com