
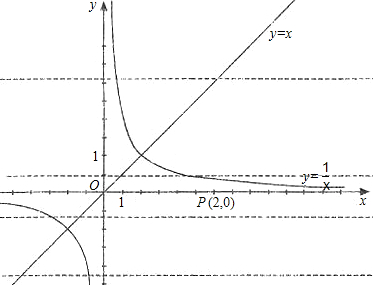
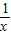 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.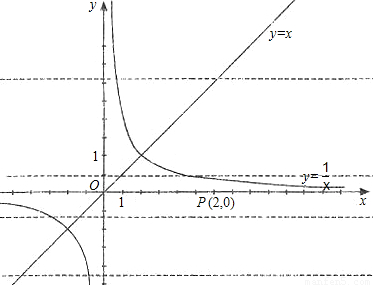
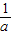 ,a)求出a值.设二次函数为y=k(x+
,a)求出a值.设二次函数为y=k(x+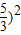 把点A代入求得k值以及函数解析式.
把点A代入求得k值以及函数解析式.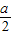 +
+ .把点A的坐标代入解析式求出a值.
.把点A的坐标代入解析式求出a值.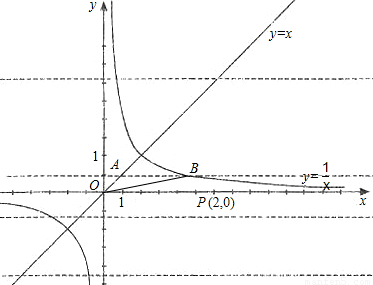
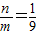 ,
,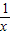 的图象上,得n=
的图象上,得n=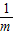 ,
, ),
), ,
, ),
), .
.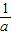 ,a),
,a),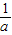 -a=
-a= ,
, .
. ,-3),
,-3), ,-
,- ),
), )2-
)2- ,
, ,
, (x+
(x+ )2-
)2-
 时,所求函数解析式为y=-
时,所求函数解析式为y=- (x-
(x- )2+
)2+ ;
;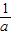 ,a),由条件可知抛物线的对称轴为x=
,a),由条件可知抛物线的对称轴为x=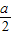 +
+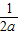 ,
, (x-2)(x-(a+
(x-2)(x-(a+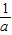 )+2),
)+2),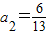 ,
, .
.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
| 1 |
| x |
| 1 |
| 9 |
| 8 |
| 3 |
| 9 |
| 5 |
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(32):2.7 最大面积是多少(解析版) 题型:解答题
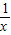 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.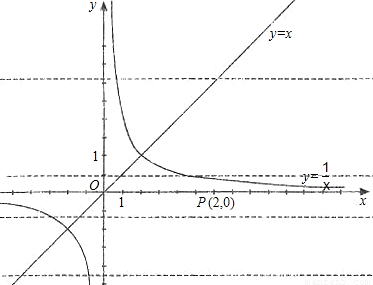
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(33):2.4 二次函数的应用(解析版) 题型:解答题
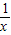 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.
查看答案和解析>>
科目:初中数学 来源:2011年北京市密云县中考数学二模试卷 (解析版) 题型:解答题
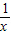 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com