
【题目】如图,已知在△ABC中,∠C=90°,AB的垂直平分线MN交BC于点D.
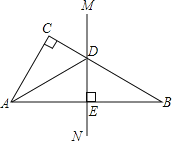
(1)如果∠CAD=20°,求∠B的度数;
(2)如果∠CAB=50°,求∠CAD的度数;
(3)如果∠CAD:∠DAB=1:2,求∠CAB的度数.
【答案】(1)∠B=35°;(2)∠CAD=10°;(3)∠CAB=54°.
【解析】试题分析:(1)根据直角三角形的性质求出∠ADC=70°,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(2)根据直角三角形的性质求出∠B的度数,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(3)设∠CAD=x,根据题意列出方程,解方程即可.
试题解析:(1)∵∠C=90°,∠CAD=20°,
∴∠ADC=70°,
∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=35°,
答:∠B的度数是35°;
(2)∵∠C=90°,∠CAB=50°,
∴∠B=40°,
∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=40°,
∴∠CAD=10°;
(3)设∠CAD=x,则∠DAB=∠B=2x,
则x+2x+2x=90°,
解得x=18,
则∠CAB=54°.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
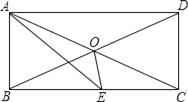
【题目】矩形ABCD中,AC、BD相交于O,AE平分∠BAD交BC于E.
(1)求证:△ABE是等腰直角三角形;
(2)若∠CAE=15°,求证:△ABO是等边三角形;
(3)在(2)的条件下,求∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=BC,将△ABC绕顶点B逆时针方向旋转![]() 度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
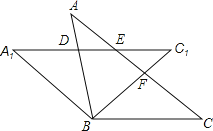
(1)若∠ABC=![]() ,∠DBF=
,∠DBF=![]() ,则
,则![]() =______°;
=______°;
(2)求证:△BCF≌△BA1D;
(3)连接DF,当∠DBF=![]() 时,判定△DBF的形状并说明理由.
时,判定△DBF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
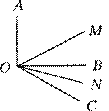
【题目】(1)已知∠AOB是直角,OM平分∠AOC,ON平分∠BOC,求∠MON与∠AOB的关系.
(2)如果(1)中,改变∠AOB的大小,其他条件不变,求∠MON与∠AOB的关系.
(3)你从(1),(2)的结果中能发现什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图![]() 示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.

(2)现在如图b示,仍有AB∥CD,但点E在AB与CD的上方,①请尝试探索∠1,∠2,∠E三者的数量关系. ②请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两瓶酒精,甲瓶有![]() 升,浓度未知;乙瓶有
升,浓度未知;乙瓶有![]() 升,浓度
升,浓度![]() ,从甲瓶中倒入乙瓶
,从甲瓶中倒入乙瓶![]() 升酒精,摇匀后倒回一部分给甲瓶,此时甲瓶浓度为
升酒精,摇匀后倒回一部分给甲瓶,此时甲瓶浓度为![]() ,乙瓶浓度为
,乙瓶浓度为![]() ,此时乙瓶中有酒精( )升.
,此时乙瓶中有酒精( )升.
A. 5 B. 6.3 C. 5.25 D. 5.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣ ![]() ;④4ac﹣b2>8a;
;④4ac﹣b2>8a;
其中正确的结论是( )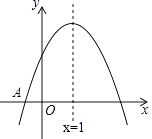
A.①③④
B.①②③
C.①②④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE=![]() AC时,求CE的长.
AC时,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m.
(1)求此时梯子的顶端A距地面的高度AC;
(2)如果梯子的顶端A下滑了0.9m,那么梯子的顶端B在水平方向上向右滑动了多远?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com