
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连结
,连结![]() ,点
,点![]() 为
为![]() 的中点,则
的中点,则![]() 的最小值为________.
的最小值为________.

科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为直径,
为直径,![]() 为弦.过
为弦.过![]() 延长线上一点
延长线上一点![]() ,作
,作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界最长的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,其中珠海站到香港站全长约55千米,2018年10月24日上午9时正式通车.一辆观光巴士自珠海站出发,25分钟后,一辆小汽车从同一地点出发,结果同时到达香港站.已知小汽车的速度是观光巴士的1.6倍,求观光巴士的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,BC交直径AD于点E,过点C作AD的垂线交AB的延长线于点G,垂足为F.连接OC.
(1)若∠G=48°,求∠ACB的度数;
(2)若AB=AE,求证:∠BAD=∠COF;
(3)在(2)的条件下,连接OB,设△AOB的面积为S1,△ACF的面积为S2.若tan∠CAF=![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E是AD边的中点,BD、CE交于点H,BE、AH交于点G,则下列结论:①AG⊥BE;②BE:BC=![]() :2;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的个数是
:2;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的个数是

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
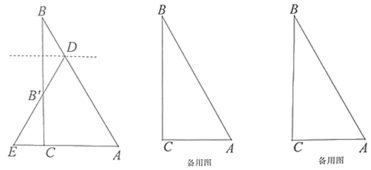
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:△DEF是等边三角形.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上,将
上,将![]() 沿着过点
沿着过点![]() 的一条直线翻折,使点
的一条直线翻折,使点![]() 落在射线
落在射线![]() 上的点
上的点![]() 处,连接
处,连接![]() 并延长,交射线
并延长,交射线![]() 于
于![]() .
.
(1)当点![]() 与点
与点![]() 重合时,求BD的长.
重合时,求BD的长.
(2)当点![]() 在
在![]() 的延长线上时,设
的延长线上时,设![]() 为
为![]() ,
,![]() 为
为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出定义域.
的函数关系式,并写出定义域.
(3)连接![]() ,当
,当![]() 是直角三角形时,请直接写出
是直角三角形时,请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义)配方法是指将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平
方式的和,这种方法称之为配方法,例如:可将多项式![]() 通过横档变形化为
通过横档变形化为![]() 的形式,这个变形过程中应用了配方法.
的形式,这个变形过程中应用了配方法.
(1)(理解)对于多项式![]() ,当x=____________时,它的最小值为______________.
,当x=____________时,它的最小值为______________.
(2)(应用)若![]() ,求
,求![]() 的值.
的值.
(3)(拓展)![]() 是
是![]() 的三边,且有
的三边,且有![]() .
.
①若c为整数,求c的值.
②直接写出这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个被平均分成![]() 等份的转盘,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为
等份的转盘,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为![]() ,乙转动转盘后指针所指区域内的数字为
,乙转动转盘后指针所指区域内的数字为![]() (当指针在边界上时,重转一次,直到指向一个区域为止).
(当指针在边界上时,重转一次,直到指向一个区域为止).
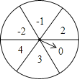
![]() 直接写出甲转动转盘后所指区域内的数字为负数的概率;
直接写出甲转动转盘后所指区域内的数字为负数的概率;
![]() 用树状图或列表法,求出点
用树状图或列表法,求出点![]() 落在第二象限内的概率.
落在第二象限内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com