
【题目】如图,矩形 ABCD 中,对角线 AC 的垂直平分线交 AD 、BC 于点 E 、F , AC 与EF 交于点O ,连结 AF 、CE 。

(1)求证:四边形 AFCE 是菱形;
(2)若 AB 4, AD 8 ,求菱形 AFCE 的边长。
【答案】(1)见解析;(2)3.
【解析】
(1)由矩形的性质得出AD∥BC,∠EAO=∠FCO,证明△AEO≌△CFO,得出AE=CF,证出四边形AFCE是平行四边形,再由对角线AC⊥EF,即可得出结论; (2)设AF=CF=x,则BF=8-x,在Rt△ABF中,根据勾股定理得出方程,解方程即可.
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠EAO=∠FCO,
∵EF是AC的垂直平分线,
∴AO=CO,∠EOA=∠FOC=90°,
在△AEO和△CFO中,
 ,
,
∴△AEO≌△CFO(ASA),
∴AE=CF,
∴四边形AFCE是平行四边形,
又∵AC⊥EF,
∴四边形AFCE是菱形;
(2)解:∵四边形AFCE是菱形,
∴AF=CF, 设AF=CF=x,则BF=8-x,
在Rt△ABF中,AF2=AB2+BF2,
即x2=42+(8-x)2, 解得 x= 3,
∴菱形AFCE的边长为3.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG,若S四边形DGBA=6,AF=![]() ,则FG的长是_____.
,则FG的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A、B两个旅游点从2010年至2014年“五、一”的旅游人数变化情况分别用实线和虚线表示.根据图中所示解答以下问题:

(1)B旅游点的旅游人数相对上一年,增长最快的是哪一年?
(2)求A、B两个旅游点从2010到2014年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天课间,顽皮的小明同学拿着老师的等腰三角板玩,不小心掉到两根柱子之间,如图所示,这一幕恰巧被数学老师看见了,于是有了下面这道题.
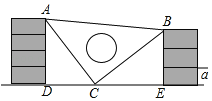
(1)求证:△ADC≌△CEB;
(2)如果每块砖的厚度a=10cm,请你帮小明求出三角板ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为 2 的正方形 ABCD 中,点 P 、Q 分别是边 AB 、 BC 上的两个动点(与点 A 、B 、C 不重合)且始终保持 BP BQ, AQ QE ,QE 交正方形外角平分线CE 于点 E , AE 交CD 于点 F ,连结 PQ 。
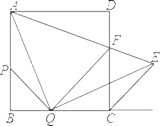
(1)求证: APQ ≌ QCE ;
(2)求QAE 的度数;
(3)设 BQ x ,当 x 为何值时, QF CE ,并求出此时AQF 的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们知道|x|的几何意义是:在数轴上数x对应的点与原点O的距离,这个结论可以推广为:|x1﹣x2|表示在数轴上数x1,x2对应点之间的距离.
例:解方程|x﹣1|+|x+2|=5.
由绝对值的几何意义知,该方程表示:求在数轴上与1和﹣2的距离之和为5的点对应的数,而在数轴上,1和﹣2的距离为|1﹣(﹣2)|=3,满足方程的x对应点在1的右边或﹣2的左边,若x对应点在1的右边,
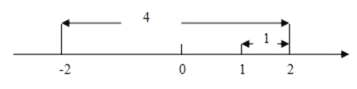
由图可知看出x=2;同理,若x对应点在﹣2的左边,可得x=﹣3,故原方程的解是x=2或x=﹣3.
参考阅读材料,解答下列问题:
(1)方程|x﹣2|+|x+3|=7的解为 .
(2)代数式|x﹣1|+|x+4|的最小值为 .
(3)如图,点A、B、C是数轴上的三点,A点表示数是-3,B点表示数是-1,C点表示数是6,点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= .(用含t的代数式表示)
![]()
(4)在(3)的条件下,若mAC﹣4AB的值不随着时间t的变化而改变,试确定m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
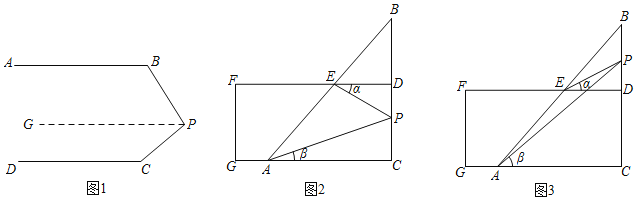
(1)如图1,已知AB∥CD,∠PBA=125°,∠PCD=155°,求∠BPC的度数.
佩佩同学的思路:过点P作PG∥AB,进而PG∥CD,由平行线的性质来求∠BPC,求得∠BPC=
问题迁移
(2)图2.图3均是由一块三角板和一把直尺拼成的图形,三角板的两直角边与直尺的两边重合,∠ACB=90°,DF∥CG,AB与FD相交于点E,有一动点P在边BC上运动,连接PE,PA,记∠PED=∠α,∠PAC=∠β.
①如图2,当点P在C,D两点之间运动时,请直接写出∠APE与∠α,∠β之间的数量关系;
②如图3,当点P在B,D两点之间运动时,∠APE与∠α,∠β之间有何数量关系?请判断并说明理由;
拓展延伸
(3)当点P在C,D两点之间运动时,若∠PED,∠PAC的角平分线EN,AN相交于点N,请直接写出∠ANE与∠α,∠β之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com