
| 比赛项目 | 演讲 | 书法 | 作文 | 手抄报 | 小品 | 漫画 |
| 参赛人数(人) | 36 | 75 | 90 | 60 | 24 | 15 |
| 比例(%) | 12 | 25 | 30 | 20 | 8 | 5 |
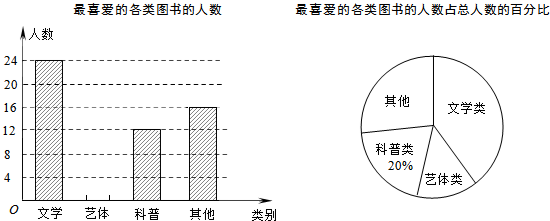
分析 (1)根据参加手抄报的人数是60人,所占的百分比是20%,即可求得总人数,进而求得其它项;
(2)根据(1)的计算即可确定总人数,根据众数的定义求得众数;
(3)根据统计表可以写出结论,答案不唯一.
解答 解:(1)参赛的总人数是:60÷20%=300(人),
则参加书法的人数是:300×25%=75(人),
参加作文比赛的比例是:$\frac{90}{300}$×100%=30%,
参加小品比赛的人数是:300×8%=24(人);
| 比赛项目 | 演讲 | 书法 | 作文 | 手抄报 | 小品 | 漫画 |
| 参赛人数(人) | 36 | 75 | 90 | 60 | 24 | 15 |
| 比例(%) | 12 | 25 | 30 | 20 | 8 | 5 |
点评 本题考查统计表的制作与从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源:2016-2017学年度海南省九年级第二次月考数学试卷(解析版) 题型:解答题
(8分)一个不透明的盒子中,装有2个白球和1个红球,这些球除颜色外其余都相同.
(1)小明认为,搅均后从中任意摸出一个球,不是白球就是红球,因此模出白球和模出红球这两个事件是等可能的. 你同意他的说法吗?为什么?
(2)搅均后从中一把模出两个球,请通过树状图或列表,求两个球都是白球的概率;
(3)搅均后从中任意模出一个球,要使模出红球的概率为 ,应如何添加红球?
,应如何添加红球?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 平均数 | 中位数 | 众数 |
| 82.6 | 89.5 | 92 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
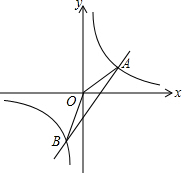 已知一次函数y=2x-k与反比例函数y=$\frac{k+2}{x}$的图象相交于A、B,其中A的横坐标为3.
已知一次函数y=2x-k与反比例函数y=$\frac{k+2}{x}$的图象相交于A、B,其中A的横坐标为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知一次函数y=kx-3的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A、B两点,点A的坐标为(4,1);
如图,已知一次函数y=kx-3的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A、B两点,点A的坐标为(4,1);查看答案和解析>>
科目:初中数学 来源: 题型:填空题
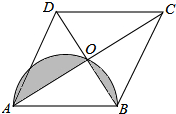 如图,菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为$\frac{25}{8}π-6$.
如图,菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为$\frac{25}{8}π-6$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\frac{{1-\sqrt{5}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com