
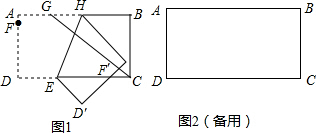
分析 如图连接EF、EF′,作F′M⊥CE于M.首先证明△CMF′∽△GBC,推出F′M:CM:CF′=3:4:5,设F′M=3k,CM=4k,CF′=5k,在Rt△EMF′中,根据EF′2=EM2+MF′2,列出方程即可解决问题.
解答 解:如图连接EF、EF′,作F′M⊥CE于M.
在Rt△DEF中,∵DF=2$\sqrt{15}$,DE=5,
∴EF=EF′=$\sqrt{D{F}^{2}+D{E}^{2}}$=$\sqrt{60+25}$=$\sqrt{85}$,
在Rt△BGC中,∵BG=$\frac{32}{3}$,BC=8,
∴CG=$\sqrt{G{B}^{2}+B{C}^{2}}$=$\frac{40}{3}$,
∴BC:BG:GC=3:4:5,
由△CMF′∽△GBC,可知F′M:CM:CF′=3:4:5,设F′M=3k,CM=4k,CF′=5k,
在Rt△EMF′中,∵EF′2=EM2+MF′2,
∴($\sqrt{85}$)2=(10-4k)2+(3k)2,
解得k=$\frac{1}{5}$或3(舍弃),
∴CF′=5k=1.
故答案为1.
点评 本题考查翻折变换、矩形的性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是学会添加辅助线,构造直角三角形,学会用构建方程的首先思考问题,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
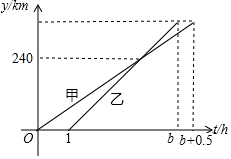 甲、乙两车从A地出发前往B地.在整个行程中,甲、乙两车离开A地的距离 y(km)与行驶的时间t(h)的关系如图所示,则A、B两地的距离为360km.
甲、乙两车从A地出发前往B地.在整个行程中,甲、乙两车离开A地的距离 y(km)与行驶的时间t(h)的关系如图所示,则A、B两地的距离为360km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | 丙 | |
| 平均货轮载重的吨数(万吨) | 10 | 5 | 7.5 |
| 平均每吨货物可获例如(百元) | 5 | 3.6 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
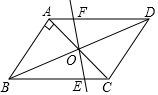 如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
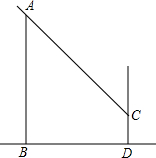 如图,一位同学想利用树影测量树(AB)的高度,他在某一时刻测得高为1米的竹竿直立时影长为0.9米,此时,因树靠近一幢建筑物,影子不全落在地面上(有一部分影子落在了墙上CD处),他先测得落在墙上的影子(CD)高为1.2米,又测得地面部分的影长(BD)为2.7米,则他测得的树高应为多少米?
如图,一位同学想利用树影测量树(AB)的高度,他在某一时刻测得高为1米的竹竿直立时影长为0.9米,此时,因树靠近一幢建筑物,影子不全落在地面上(有一部分影子落在了墙上CD处),他先测得落在墙上的影子(CD)高为1.2米,又测得地面部分的影长(BD)为2.7米,则他测得的树高应为多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com