
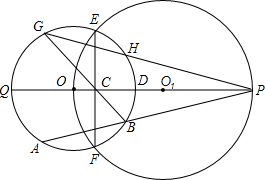
 如图,⊙O1经过⊙O的圆心,E、F是两圆的交点,直线OO1交⊙O于点Q、D,交⊙O1于点P,交EF于点C,点A在劣弧QF上运动(与点Q、F不重合),连结PA交弧DF于B,连结BC并延长交⊙O于点G,连结PG交⊙O于点H.求证:
如图,⊙O1经过⊙O的圆心,E、F是两圆的交点,直线OO1交⊙O于点Q、D,交⊙O1于点P,交EF于点C,点A在劣弧QF上运动(与点Q、F不重合),连结PA交弧DF于B,连结BC并延长交⊙O于点G,连结PG交⊙O于点H.求证:分析 (1)连接PE、OE,如图1,要证PE是⊙O的切线,只需证∠OEP=90°,只需证OP是⊙O1的直径即可;
(2)连接PE、OE、OG、OA、OB,如图2,要证PA=PG,只需证△OGP≌△OAP,只需证∠GOP=∠POA.易证△PCE∽△PEO,根据相似三角形的性质可得PE2=PC•PO,同理OE2=OC•OP.根据切割线定理可得PE2=PB•PA,则有PC•PO=PB•PA,由此可证到△BPC∽△OPA,则有∠PBC=∠POA.要证∠GOP=∠POA,只需证∠GOP=∠PBC,只需证∠OPB=∠OGB,由OG=OB可得∠OBC=∠OGB,只需证∠OBC=∠OPB,只需证△BOC∽△POB,只需证$\frac{OB}{OC}$=$\frac{OP}{OB}$,即证OB2=OC•OP,由于OB=OE,只需证OE2=OC•OP即可.
解答 证明:(1)连接PE、OE,如图1,
∵OP是⊙O1的直径,∴∠OEP=90°,
∴PE是⊙O的切线;
(2)连接PE、OE、OG、OA、OB,如图2,
∵OP⊥EF,∠OEP=90°,
∴∠OCE=∠ECP=∠OEP=90°.
∵∠EPC=∠OPE,
∴△PCE∽△PEO,
∴$\frac{PE}{PO}$=$\frac{PC}{PE}$,即PE2=PC•PO,
同理OE2=OC•OP.
∵PE是⊙O的切线,
∴根据切割线定理可得PE2=PB•PA,
∴PC•PO=PB•PA,
∴$\frac{PC}{PB}$=$\frac{PA}{PO}$
∵∠BPC=∠OPA,
∴△BPC∽△OPA,
∴∠PBC=∠POA.
∵OE2=OC•OP,OE=OB,
∴OB2=OC•OP,即$\frac{OB}{OC}$=$\frac{OP}{OB}$.
∵∠BOC=∠POB,
∴△BOC∽△POB,
∴∠OBC=∠OPB.
∵OG=OB,∴∠OBC=∠OGB,
∴∠OPB=∠OGB,
∴∠GOP=180°-∠OGB-OCG=180°-∠OPB-∠BCP=∠PBC,
∴∠GOP=∠PBC=∠POA.
在△OGP和△OAP中,
$\left\{\begin{array}{l}{OG=OA}\\{∠GOP=∠AOP}\\{OP=OP}\end{array}\right.$,
∴△OGP≌△OAP,
∴PG=PA.
点评 本题主要考查了圆周角定理、切线的判定、相似三角形的判定与性质、全等三角形的判定与性质、切割线定理、等腰三角形的性质、三角形内角和定理等知识,解决本题的关键是把证明∠GOP=∠POA转化为证明∠GOP=∠PBC=∠POA,进而把证明∠GOP=∠PBC转化为证明∠BPC=∠OGC=∠OBC.


科目:初中数学 来源: 题型:解答题
 如图所示,在等腰梯形ABCD中,AB∥CD,AD=BC,AC与BD交于点0,∠AOB=60°,P、Q、R分别是OA、BC、OD的中点.求证:△PQR是正三角形.
如图所示,在等腰梯形ABCD中,AB∥CD,AD=BC,AC与BD交于点0,∠AOB=60°,P、Q、R分别是OA、BC、OD的中点.求证:△PQR是正三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,用长为50米的篱笆囤成一个养鸡场,养鸡场的一面靠墙.问:(1)如何围,才能使养鸡场的面积最大?
如图,用长为50米的篱笆囤成一个养鸡场,养鸡场的一面靠墙.问:(1)如何围,才能使养鸡场的面积最大?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com