
【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图像与性质,研究过程如下,请补充完整.
的图像与性质,研究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
|
|
| 10 |
| -2 | 1 |
| 1 | -2 | 3 | 10 |
|
其中,![]() _______,
_______,![]() =________;
=________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图像;
(3)观察函数图像:
①写出函数的一条图像性质:__________;
②当方程![]() 有且仅有两个不相等的实数根,根据函数图像直接写出
有且仅有两个不相等的实数根,根据函数图像直接写出![]() 的取值范围为________.
的取值范围为________.
【答案】(1)3;2;(2)图像见解析;①图像具有对称性,对称轴是直线![]() (或当
(或当![]() 或
或![]() 时,函数的最小值是-2,答案不唯一),②
时,函数的最小值是-2,答案不唯一),②![]() 或
或![]() .
.
【解析】
(1)将![]() ,
,![]() 代入函数解析式即可求出m,n的值;
代入函数解析式即可求出m,n的值;
(2)利用表格数据描点,再用平滑的曲线连接即可;
(3)①从图象与坐标轴的交点,图象的对称性,对称轴,增减性等方面写出一条性质即可;
②根据函数![]() 与
与![]() 有两个交点,结合图像即可得出答案.
有两个交点,结合图像即可得出答案.
(1)当![]() 时,
时,![]()
∴![]()
当![]() 时,
时,![]()
∴![]()
故答案为:3,2;
(2)图像如下:
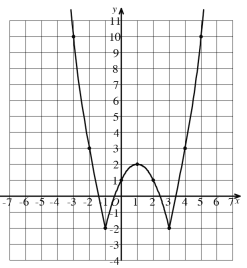
(3)①图像具有对称性,对称轴是直线![]() (或当
(或当![]() 或
或![]() 时,函数的最小值是-2,答案不唯一)
时,函数的最小值是-2,答案不唯一)
②方程![]() 可变形为
可变形为![]() ,
,
故找到函数![]() 与
与![]() 有两个交点的情况即可,
有两个交点的情况即可,
由图像可知,当![]() 或
或![]() 时,
时,
函数![]() 与
与![]() 有两个交点,
有两个交点,
故答案为:![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】图1和图2中的正方形ABCD和四边形AEFG都是正方形.
(1)如图1,连接DE,BG,M为线段BG的中点,连接AM,探究AM与DE的数量关系和位置关系,并证明你的结论;
(2)在图1的基础上,将正方形AEFG绕点A逆时针方向旋转到图2的位置,连结DE、BG,M为线段BG的中点,连结AM,探究AM与DE的数量关系和位置关系,并证明你的结论.
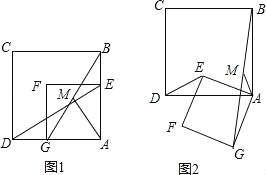
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 满足的反比例函数关系如图2所示,等腰直角三角形
满足的反比例函数关系如图2所示,等腰直角三角形![]() 的斜边
的斜边![]() 过
过![]() 点,点
点,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() 为
为![]() 的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )
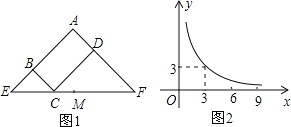
A.当![]() 时,
时,![]()
B.当![]() 时,
时,![]()
C.当![]() 增大时,
增大时,![]() 的值增大
的值增大
D.当![]() 增大时,
增大时,![]() 的值不变
的值不变
查看答案和解析>>
科目:初中数学 来源: 题型:
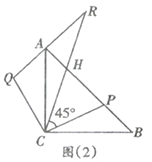
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上(
上(![]() ),作
),作![]() ,且
,且![]() ,连接
,连接![]() ,如图(1).
,如图(1).
(1)求证:![]() ;
;
(2)延长![]() 至点
至点![]() ,使得
,使得![]() ,
,![]() 与
与![]() 交于点
交于点![]() .如图(2).
.如图(2).
①求证:![]() ;
;
②求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
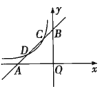
【题目】如图,已知直线![]() 与x轴、y轴分别交于点A,B,与双曲线
与x轴、y轴分别交于点A,B,与双曲线![]() 分别交于点C,D,且点C的坐标为
分别交于点C,D,且点C的坐标为![]() .
.
(1)分别求出直线、双曲线的函数表达式.
(2)求出点D的坐标.
(3)利用图象直接写出:当x在什么范围内取值时![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并按要求解决问题: 问题:“在平面内,已知分别有![]() 个点,
个点,![]() 个点,
个点,![]() 个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
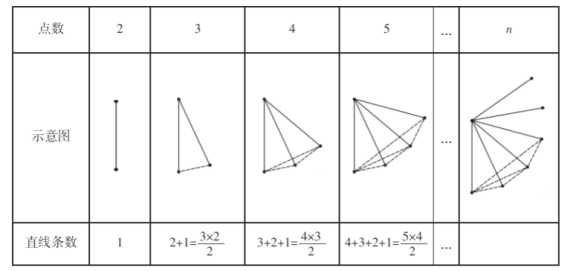
请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有![]() 个点时,直线条数为 ;
个点时,直线条数为 ;
(2)若某同学按照本题中的方法,共画了![]() 条直线,求该平面内有多少个已知点.
条直线,求该平面内有多少个已知点.
查看答案和解析>>
科目:初中数学 来源: 题型:
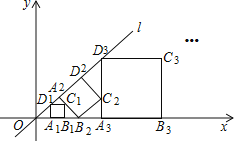
【题目】如图,在平面直角坐标系中,直线l为正比例函数y=x的图象,点A1的坐标为(1,0),过点A1作x轴的垂线交直线l于点D1,以A1D1为边作正方形A1B1C1D1;过点C1作直线l的垂线,垂足为A2,交x轴于点B2,以A2B2为边作正方形A2B2C2D2;过点C2作x轴的垂线,垂足为A3,交直线l于点A3,以A3D3为边作正方形A3B3C3D3,…,按此规律操作下所得到的正方形A2019B2019C2019D2019的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com