
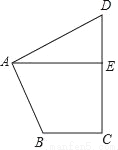
��ͼ�����ı���ABCD�У���BAD=��C=90�㣬AB=AD��AE��CD������ΪE�����߶�AE=10����S�ı���ABCD=_____��
 ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ������
������һ�߳�Ϊ10�������߳��Ƿ���x2-14x+48=0��������������һ�� ������.
ֱ�� ���������������� �ⷽ�̵� �� �����������Ϊֱ���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�걱ʦ������꼶��ѧ�ϲ��5�� һԪһ�η��� ��Ԫ���Ծ� ���ͣ������
��������������ƶ��绰�Ʒѷ�ʽ��������������⣺
ȫ��ͨ | ������ | |
����� | 25Ԫ/�� | 0 |
����ͨ���� | 0.2Ԫ/���� | 0.3Ԫ/���� |
(1)һ�����ڱ���ͨ�����ٷ���ʱ������ͨѶ��ʽ�ķ�����ͬ��
(2)��ij��Ԥ��һ������ʹ�ñ���ͨ����90Ԫ����Ӧ��ѡ������ͨѶ��ʽ�Ϻ��㣿
(1) 250����;(2) ѡ��ȫ��ͨ�ȽϺ��㣮 �������������������1���ӱ����п�֪��ȫ��ͨ����25Ԫ��ÿ��һ����0.2Ԫ��������û�����⣬ÿ����0.3Ԫ����˿���һ�����ڱ���ͨ��x����ʱ����������ͨѶ��ʽ�ķ�����ͬ�г�������⼴�ɣ� ��2���ֱ��з���������ּƷѷ�ʽ����ͨ������90Ԫʱ��ͨ��ʱ�䣬Ȼ����бȽϼ��ɵó����ۣ� ��������� �������� ��1����һ�����ڱ���ͨ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�걱ʦ������꼶��ѧ�ϲ��5�� һԪһ�η��� ��Ԫ���Ծ� ���ͣ���ѡ��
ij����Ʒ�������۳��ۣ������ԭ���۵������۳��ۣ�����25Ԫ������ԭ���۵ľ��۳��ۣ���20Ԫ����������Ʒ��ԭ����(����)
A. 500Ԫ B. 400Ԫ C. 300Ԫ D. 200Ԫ
C ���������������� ��������Ʒ��ԭ����xԪ����������ã�75%x+25=90%x��20�����x=300����ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������Т����2016-2017ѧ����꼶���ϣ���ĩ������ѧ�Ծ� ���ͣ������
�Ķ����в��ϣ������Ӧѧϰ����
�ĵ㹲Բ������
����֪����������һ�������ε�������������һ��Բ��������һ���ı��ε��ĸ���������һ��Բ��С������ʵ��̽�����֣����Խǻ������ı��ε��ĸ���������һ��Բ��������С�����÷�֤��֤����������Ĺ��̣�
��֪�����ı���ABCD�У���B+��D=180�㣮
��֤������A��B��C��D����һ��Բ��
֤������ͼ��1�����������A��B��C��D�ĵ㲻����һ��Բ����A��B��C������Բ������D��Բ�⣬��AD��Բ�ཻ�ڵ�E������CE������B+��AEC=180��������֪��B+��D=180�㣬���ԡ�AEC=��D������AEC�ǡ�CED����ǣ���AEC����D������ì�ܣ��ʼ��費��������˵�D�ڹ�A��B��C�����Բ�ϣ�
��ͼ��2���������A��B��C��D�ĵ㲻����һ��Բ����A��B��C������Բ������D��Բ�ڣ���AD���ӳ�����Բ�ཻ�ڵ�E������CE������B+��AEC=180��������֪��B+��ADC=180�㣬���ԡ�AEC=��ADC������ADC�ǡ�CED����ǣ���ADC����AEC������ì�ܣ��ʼ��費��������˵�D�ڹ�A��B��C�����Բ�ϣ�
��˵õ��ĵ㹲Բ�����������Խǻ������ı��ε��ĸ���������һ��Բ��
ѧϰ����
��1�������л��߲��ֽ��۵��������� ����
��2��֤����������Ҫ����������������ѧ˼�룺�� ��������ĸ���ż��ɣ�
A������˼�� B������˼�� C�����ν��˼�� D����������˼��
��3����ͼ��3�������ı���ABCD�У���ABC=��ADC=90�㣬��CAD=16�㣮AD=BD�������ADB�Ĵ�С��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������Т����2016-2017ѧ����꼶���ϣ���ĩ������ѧ�Ծ� ���ͣ���ѡ��
�ƽ�ָ����ʵ���������й㷺��Ӧ�ã�����������������ʱ��ʹ������ϲ��������ϣ����²��������£��ĸ߶ȱȣ������²���ȫ����ȫ�����ĸ߶ȱȣ����������Ӿ����У����˱������������ĸ�Ϊ2m�������²�Ϊx�ף������й���x�ķ�����ȷ���ǣ�������
A. x2+2x��4=0 B. x2��2x��4=0 C. x2��6x+4=0 D. x2��6x��4=0
A ������������������������²�Ϊx�ף����õ�����ϲ��������ϣ����²��������£��ĸ߶ȱȣ������²���ȫ����ȫ�����ĸ߶ȱȿɵã� ������x2��2x��4��0�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������Т����2016-2017ѧ����꼶���ϣ���ĩ������ѧ�Ծ� ���ͣ���ѡ��
��֪����������y= ��������������ͼ�����ڵ�ÿһ�������ڣ�y��ֵ����x�������������ôk��ȡֵ�����ǣ�������
��������������ͼ�����ڵ�ÿһ�������ڣ�y��ֵ����x�������������ôk��ȡֵ�����ǣ�������
A. 0 B. 2 C. 3 D. 4
A ������������������߷���������y����������������ͼ�����ڵ�ÿһ�������ڣ�y��ֵ����x����������� ��k��1��0�� ��k��1������k���ܵ�ȡֵֻ����0�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ������
��������x�ύ�ڵ㣨1��0��������3��0������������߿���Ϊ��_____��
y=a��x��1����x+3����a��0�� ���������������������������x�ύ�ڵ㣨1��0������-3��0���� ����������߽���ʽΪ��y=a��x-1����x+3����a��0���� �ʴ��ǣ�y=a��x-1����x+3����a��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ݵ���2017-2018ѧ��ȵ�һѧ����ĩ�����꼶��ѧ�Ծ� ���ͣ������
��1���ֽ���ʽ����  �� ��
�� �� ��
��
��2����֪a+b=2,�� ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com