
 张师傅要在如图所示的钝角三角形铁片上截取一个面积最大的半圆形工件,如果要求半圆形工件的直径恰好在三角形铁片的最长边上.
张师傅要在如图所示的钝角三角形铁片上截取一个面积最大的半圆形工件,如果要求半圆形工件的直径恰好在三角形铁片的最长边上.分析 (1)作∠BAC的平分线AD,交BC边于点O,过点O作OW⊥AC,以点O为圆心,OW为半径画半圆即可;
(2)过点O作OE⊥AB于点E,则OE=OW=r,再由∠B=30°,∠C=45°用r表示出OB及OC的长,再根据BC=a即可得出结论.
解答 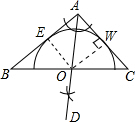 解:(1)如图所示;
解:(1)如图所示;
(2)过点O作OE⊥AB于点E,则OE=OW=r,
∵∠B=30°,∠C=45°,
∴OB=2r,OC=$\sqrt{2}$r.
∵BC=a,
∴2r+$\sqrt{2}$r=a,解得r=$\frac{(2-\sqrt{2})a}{2}$.
点评 此题主要考查的是作图-应用与设计作图,实质是作一个与钝角三角形两边相切,直径在三角开最长边且面积最大的半圆,解这类题要善于从实际情景中抽象出相应数学模型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com