
【题目】已知当x1=a,x2=b,x3=c时,二次函数y= ![]() x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 .
x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 .
【答案】m>﹣ ![]()
【解析】方法一: 解:∵正整数a,b,c恰好是一个三角形的三边长,且a<b<c,
∴a最小是2,
∵y1<y2<y3 ,
∴﹣ ![]() <2.5,
<2.5,
解得m>﹣2.5.
方法二:
解:当a<b<c时,都有y1<y2<y3 ,
即 ![]() ,
,
∴ 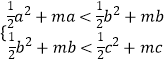 ,
,
∴ 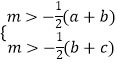 ,
,
∵a,b,c恰好是一个三角形的三边长,a<b<c,
∴a+b<b+c,
∴m>﹣ ![]() (a+b),
(a+b),
∵a,b,c为正整数,
∴a,b,c的最小值分别为2、3、4,
∴m>﹣ ![]() (a+b)≥﹣
(a+b)≥﹣ ![]() (2+3)=﹣
(2+3)=﹣ ![]() ,
,
∴m>﹣ ![]() ,
,
故答案为:m>﹣ ![]() .
.
根据三角形的任意两边之和大于第三边判断出a最小为2,再根据二次函数的增减性和对称性判断出对称轴在2、3之间偏向2,即小于2.5,然后列出不等式求解即可.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读与思考 婆罗摩笈多(Brahmagupta),是一位印度数学家和天文学家,书写了两部关于数学和天文学的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数概念及加减法运算仅晚于中国《九章算术》,而他的负数乘除法法则在全世界都是领先的,他还提出了著名的婆罗摩笈多定理,该定理的内容及部分证明过程如下:
已知:如图1,四边形ABCD内接于⊙O,对角线AC⊥BD于点P,PM⊥AB于点M,延长MP交CD于点N,求证:CN=DN.
证明:在△ABP和△BMP中,∵AC⊥BD,PM⊥AB,
∴∠BAP+∠ABP=90°,∠BPM+∠MBP=90°.
∴∠BAP=∠BPM.
∵∠DPN=∠BPM,∠BAP=∠BDC.
∴…
(1)请你阅读婆罗摩笈多定理的证明过程,完成剩余的证明部分.
(2)已知:如图2,△ABC内接于⊙O,∠B=30°,∠ACB=45°,AB=2,点D在⊙O上,∠BCD=60°,连接AD,与BC交于点P,作PM⊥AB于点M,延长MP交CD于点N,则PN的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西绵山是中国历史文化名山,因春秋时期晋国介子推携母隐居于此被焚而著称,如图1,是绵山上介子推母子的塑像,某游客计划测量这座塑像的高度,由于游客无法直接到达塑像底部,因此该游客计划借助坡面高度来测量塑像的高度;如图2,在塑像旁山坡坡脚A处测得塑像头顶C的仰角为75°,当从A处沿坡面行走10米到达P处时,测得塑像头顶C的仰角刚好为45°,已知山坡的坡度i=1:3,且O,A,B在同一直线上,求塑像的高度.(侧倾器高度忽略不计,结果精确到0.1米,参考数据:cos75°≈0.3,tan75°≈3.7, ![]() ≈1.4,
≈1.4, ![]() ≈1.7,
≈1.7, ![]() ≈3.2)
≈3.2)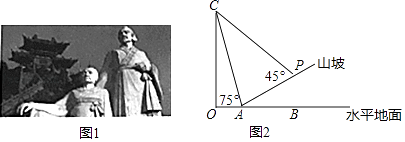
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点,(点A在点B的左侧),与直线AC交于点C(2,3),直线AC与抛物线的对称轴l相交于点D,连接BD.
(1)求抛物线的函数表达式,并求出点D的坐标;
(2)如图2,若点M、N同时从点D出发,均以每秒1个单位长度的速度分别沿DA、DB运动,连接MN,将△DMN沿MN翻折,得到△D′MN,判断四边形DMD′N的形状,并说明理由,当运动时间t为何值时,点D′恰好落在x轴上?
(3)在平面内,是否存在点P(异于A点),使得以P、B、D为顶点的三角形与△ABD相似(全等除外)?若存在,请直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2014年3月份在某医院出生的20名新生婴儿的体重如下(单位:kg)
4.7 2.9 3.2 3.5 3.8 3.4 2.8 3.3 4.0 4.5
3.6 4.8 4.3 3.6 3.4 3.5 3.6 3.5 3.7 3.7
(1)求这组数据的极差;
(2)若以0.4kg为组距,对这组数据进行分组,制作了如下的“某医院2014年3月份20名新生婴儿体重的频数分布表”(部分空格未填),请在频数分布表的空格中填写相关的量
某医院2014年3月份20名新生儿体重的频数分布表
组别(kg) | 划记 | 频数 |
略 | ||
略 | ||
3.55﹣3.95 | 正一 | 6 |
略 | ||
略 | ||
略 | ||
合计 | 20 | |
(3)经检测,这20名婴儿的血型的扇形统计图如图所示(不完整),求:
①这20名婴儿中是A型血的人数;
②表示O型血的扇形的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中的数阵是由全体正奇数排成的.
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在图中任意作一个类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由.这九个数之和能等于2 016吗?2 015,2 025呢?若能,请写出这九个数中最小的一个;若不能,请说出理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com