
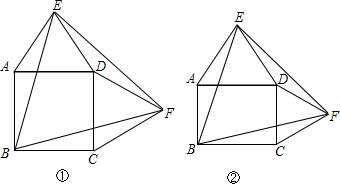
分析 (1)①利用SAS即可证明两三角形的全等;②再证明△ABE≌△DFE,可得△BEF是等边三角形;
(2)求出∠BAE,∠EDF,∠FCB的度数,继而证明△ABE≌△CFB≌△DFE,即可得出结论;
(3)证明方法与(2)完全相同,画出图形写出结论即可.
解答 ①证明:∠BAE=90°+60°=150°,∠FCB=90°+60°=150°,
在△ABE和△CFB中,
$\left\{\begin{array}{l}{AB=CF}\\{∠BAE=∠FCB}\\{AE=CB}\end{array}\right.$,
∴△ABE≌△CFB(SAS).
②∠FDE=360°-60°-60°-90°=150°,
在△ABE和△DFE中,
$\left\{\begin{array}{l}{AB=DF}\\{∠BAE=∠FDE}\\{AE=DE}\end{array}\right.$,
∴△ABE≌△DFE(SAS),
∴BE=FE,
又∵△ABE≌△CFB,
∴BE=FB=FE,
∴△BFE是等边三角形.
(2)∠BAE=90°+60°=150°,∠FCB=90°+60°=150°,∠FDE=360°-60°-60°-90°=150°,
在△ABE和△CFB中,
$\left\{\begin{array}{l}{AB=CF}\\{∠BAE=∠FCB}\\{AE=CB}\end{array}\right.$,
∴△ABE≌△CFB(SAS),
在△ABE和△DFE中,
$\left\{\begin{array}{l}{AB=DF}\\{∠BAE=∠FDE}\\{AE=DE}\end{array}\right.$,
∴△ABE≌△DFE(SAS),
∴△ABE≌△CFB≌△DFE,
∴BE=EF=FB,
∴两结论成立.
(3)将题目(1)条件中的正方形ABCD改为?ABCD,
当平行四边形中有一个角是60°时,(1)的第一个结论中的两个三角形是不存在的;第二个结论依然成立;
当平行四边形中没有60°角时,(1)的两个结论依然成立.
如图:
点评 本题考查了四边形的综合,涉及了全等三角形的判定与性质,解答本题的关键之处在于判断∠BAE=∠EDF=∠FCB,难度一般.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AC=50m,BC=40m,点A开始沿AC边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着CB匀速移动,几秒后,△PCQ与△ABC相似?
如图,在△ABC中,AC=50m,BC=40m,点A开始沿AC边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着CB匀速移动,几秒后,△PCQ与△ABC相似?查看答案和解析>>
科目:初中数学 来源: 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,E,F分别为AD,BC上两点,且BF=DE,连AF,CE,BE,DF,AF与BE交于M,DF与CE交于N,求证:四边形FMEN为平行四边形.
如图,在?ABCD中,E,F分别为AD,BC上两点,且BF=DE,连AF,CE,BE,DF,AF与BE交于M,DF与CE交于N,求证:四边形FMEN为平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com