
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ��� ![]() ��mΪ��������ͼ����x�ύ�ڵ�A����3��0������y�ύ�ڵ�C����ֱ��x=1Ϊ�Գ����������y=ax2+bx+c��a��b��cΪ��������a��0������A��C���㣬����x��������ύ�ڵ�B��
��mΪ��������ͼ����x�ύ�ڵ�A����3��0������y�ύ�ڵ�C����ֱ��x=1Ϊ�Գ����������y=ax2+bx+c��a��b��cΪ��������a��0������A��C���㣬����x��������ύ�ڵ�B��
��1����m��ֵ�������ߵĺ�������ʽ��
��2����E��y���Ҳ���������һ�㣬����E��ֱ��AC��ƽ���߽�x���ڵ�F���Ƿ���������ĵ�E��ʹ����A��C��E��FΪ������ı�����ƽ���ı��Σ������ڣ������E�����꼰��Ӧ��ƽ���ı��ε�������������ڣ���˵�����ɣ�
��3����P�������߶Գ�����ʹ��ACP���ܳ�ȡ����Сֵ�ĵ㣬����P������һ����y�ƽ�е�ֱ�߽���������M1��x1 �� y1����M2��x2 �� y2�����㣬��̽�� ![]() �Ƿ�Ϊ��ֵ����д��̽�����̣�
�Ƿ�Ϊ��ֵ����д��̽�����̣�
���𰸡�
��1��
�⣺�� ![]() �����㣨��3��0����
�����㣨��3��0����
��0=- ![]() +m�����m=
+m�����m= ![]() ��
��
��ֱ�߽���ʽΪ ![]() ��C��0��
��C��0�� ![]() ����
����
��������y=ax2+bx+c�Գ���Ϊx=1������x�ύ��A����3��0����
����һ����ΪB��5��0����
�������߽���ʽΪy=a��x+3����x��5����
�������߾���C��0�� ![]() ����
����
�� ![]() =a3����5�������a=-
=a3����5�������a=- ![]() ��
��
�������߽���ʽΪy=- ![]() x2+
x2+ ![]() x+
x+ ![]()
��2��
�⣺������ڵ�Eʹ����A��C��E��FΪ������ı�����ƽ���ı��Σ�
��AC��EF��AC=EF�����ͼ1��
��i������E�ڵ�Eλ��ʱ������E��EG��x���ڵ�G��
��AC��EF�����CAO=��EFG��
�֡� 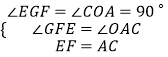 ��
��
���CAO�ա�EFG��
��EG=CO= ![]() ����yE=
����yE= ![]() ��
��
�� ![]() =-
=- ![]() xE2+
xE2+ ![]() xE+
xE+ ![]() �����xE=2��xE=0��C���غϣ���ȥ����
�����xE=2��xE=0��C���غϣ���ȥ����
��E��2�� ![]() ����SACEF=
����SACEF= ![]() ��
��
��ii������E�ڵ�E��λ��ʱ������E����E��G���x���ڵ�G�䣬
ͬ�������E�䣨 ![]() +1��-
+1��- ![]() ����SACF��E��=
����SACF��E��= ![]()
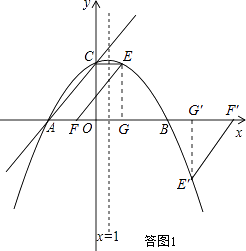
��3��
�⣺Ҫʹ��ACP���ܳ���С��ֻ��AP+CP��С���ɣ�
���ͼ2������BC��x=1��P�㣬��Ϊ��A��B����x=1�Գƣ�������Գ������Լ�����֮���߶���̣���֪��ʱAP+CP��С��AP+CP��СֵΪ�߶�BC�ij��ȣ���
��B��5��0����C��0�� ![]() ����
����
��ֱ��BC����ʽΪy=- ![]() x+
x+ ![]() ��
��
��xP=1����yP=3����P��1��3����
�����P��1��3����ֱ��Ϊy=kx+b����k+b=3����b=3��k��
��ֱ�ߵĽ���ʽ�ǣ�y=kx+3��k��
��y=kx+3��k��y=- ![]() x2+
x2+ ![]() x+
x+ ![]() ��
��
��������ã�x2+��4k��2��x��4k��3=0��
��x1+x2=2��4k��x1x2=��4k��3��
��y1=kx1+3��k��y2=kx2+3��k��
��y1��y2=k��x1��x2����
�����������빫ʽ�õ���
M1M2= ![]() =
= ![]() =
= ![]()
��M1M2= ![]() =
= ![]() =4��1+k2����
=4��1+k2����
��M1P= ![]() =
= ![]() =
= ![]() ��
��
ͬ��M2P= ![]()
��M1PM2P=��1+k2�� ![]() =��1+k2��
=��1+k2�� ![]() =��1+k2��
=��1+k2�� ![]() =4��1+k2����
=4��1+k2����
��M1PM2P=M1M2��
�� ![]() =1Ϊ��ֵ��
=1Ϊ��ֵ��
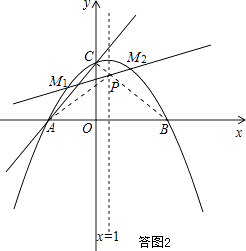
����������1���������m��ֵ��ֱ�ߵĽ���ʽ�����������߶Գ��Եõ�B�����꣬����A��B���������ý���ʽ��������ߵĽ���ʽ����2�����ڵ�Eʹ����A��C��E��FΪ������ı�����ƽ���ı��Σ����ͼ1��ʾ������E��EG��x���ڵ�G������ȫ�������Σ�����ȫ�������κ�ƽ���ı��ε��������E�������ƽ���ı��ε������ע�⣺����Ҫ���E�������������ͼ1��ʾ����Ҫ©�⣻��3�����ʽ�Ϊ���ӣ����ͼ2��ʾ���ּ�����������
��1����ȷ����ʱ��ACP���ܳ���С��������ԳƵ����ʺ�����֮���߶���̵�ԭ���������2����ȷ��P������P��1��3�����Ӷ�ֱ��M1M2�Ľ���ʽ���Ա�ʾΪy=kx+3��k����3�������ø���ϵ����ϵ���M1��M2���������Ĺأ��õ�x1+x2=2��4k��x1x2=��4k��3����һ����Ϊ�˺����ĸ��Ӽ�����������4�������������ľ��빫ʽ���ֱ�����߶�M1M2��M1P��M2P�ij��ȣ���Ƚϼ��ɵõ����ۣ� ![]() =1Ϊ��ֵ����һ���漰���������㣬ע�ⲻҪ�������������Եó����Ľ��ۣ�
=1Ϊ��ֵ����һ���漰���������㣬ע�ⲻҪ�������������Եó����Ľ��ۣ�


 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������һ��ͼ�Σ�ͨ����ͬ�ķ�������ͼ�ε�������Եõ�һ����ѧ��ʽ��
���磺��ͼ1�ɵõ�(a+b)=a+2ab+b��



ͼ1 ͼ2 ͼ3
��1��д����ͼ2����ʾ����ѧ��ʽ��_____________________��д����ͼ3����ʾ����ѧ��ʽ��_____________________��
��2�������������ۣ�����������⣺��֪a+b+c=11��bc+ac+ab=38����a+b+c��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���A=100�㣬��C=70�㣬��M��N�ֱ���AB��BC�ϣ�����BMN��MN���ۣ��á�FMN����MF��AD��FN��DC�����B�Ķ���Ϊ___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����������ABCD�У�G��CD��һ�㣬�ӳ�BC��E��ʹCE=CG������BG���ӳ���DE��F��
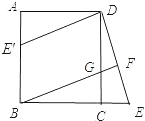
��1����֤����BCG�ա�DCE��
��2������DCE�Ƶ�D˳ʱ����ת90���õ���DAE�����ж��ı���E��BGD��ʲô�����ı��Σ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���D��E�ֱ��ڱ�AC��BC�ϣ������A��B��C�غϣ�����P��ֱ��AB�ϵ�����һ�㣨�����A��B�غϣ������PDA=x����PEB=y����DPE=m����C=n��
��1����ͼ������P���߶�AB���˶�����n=90��ʱ
����PD��BC��PE��AC����m=_____��
����m=50�㣬��x+y��ֵ��
��2������P��ֱ��AB���˶�ʱ��ֱ��д��x��y��m��n֮���������ϵ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������EFGH��������ABCD��ij����ת�õ����������Ϊ��ת���ĵ��ǣ� �� 
A.M��O��N
B.E��O��C
C.E��O��N
D.M��O��C
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龰��
��ͼ1��AB//CD����PAB=130�㣬��PCD=120�������APC�Ķ�����

С����˼·�ǣ�
����P��PE//AB��

���PAB+��APE=180�㣮
�ߡ�PAB=130�㣬���APE=50��
��AB//CD��PE//AB����PE//CD��
���PCD+��CPE=180�㣮
�ߡ�PCD=120�㣬���CPE=60��
���APC=��APE+��CPE=110�㣮
����Ǩ�ƣ�
���AB��CDƽ�й�ϵ���䣬����P��ֱ��AB��CD���������ڲ��˶�ʱ����PAB����PCD�Ķ�������ŷ����仯��
��1����ͼ3��������P�˶���ֱ��AC�Ҳ�ʱ����д����PAB����PCD�͡�APC֮���������ϵ����˵�����ɣ�

��2����ͼ4��AQ��CQ�ֱ�ƽ�֡�PAB����PCD����ô��AQC�ͽǡ�APC�������������ϵ��

��3����ͼ5����P��ֱ��AC�����ʱ��AQ��CQ��Ȼƽ�֡�PAB����PCD����ֱ��д����AQC�ͽǡ�APC��������ϵ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬ����ѧΪ�ḻѧ����У������Ӿ�Ծ������Ʒ�̵�һ���Թ������ɸ����������ÿ������ļ۸���ͬ��ÿ������ļ۸���ͬ����������3�������2��������310Ԫ������2�������5��������500Ԫ��
��1������һ������һ������������Ԫ��
��2������ͬ����ѧ��ʵ���������Ӿ�Ծ������Ʒ�̵�һ���Թ������������96����Ҫ���������������ܷ��ò�����5720Ԫ��������ѧ�����Թ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯���꼶ѧ���μӺ�����д�������������ȡ����ѧ���ɼ���Ϊ�������з��������Ƴ����µ�ͳ�Ʊ���


�����������Ϣ������������⣺
��1��a=__________��b=__________��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����֪���꼶��400��ѧ���μ���α��������ɼ���90�����ϣ���90�֣���Ϊ�ţ����Ƹ��꼶�ɼ�Ϊ�ŵ��ж����ˣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com