

分析 (1)根据A的人数为105人,所占的百分比为35%,求出总人数,即可解答;
(2)C所对应的人数为:总人数×30%,B所对应的人数为:总人数-A所对应的人数-C所对应的人数-D所对应的人数,即可解答;
(3)根据B所占的百分比×360°,即可解答;
(4)根据概率公式,即可解答.
解答 解:(1)105÷35%=300(人).
故答案为:300;
(2)n=300×30%=90(人),m=300-105-90-45=60(人).
故答案为:60,90;
(3)$\frac{60}{300}$×360°=72°.
故答案为:72°;
(4)从该校学生中随机抽取一个最关注热词D的学生的概率是$\frac{45}{300}$=$\frac{3}{20}$.
答:从该校学生中随机抽取一个最关注热词D的学生的概率是$\frac{3}{20}$.
点评 本题考查条形统计图与扇形统计图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.也考查了概率的求法与运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.
如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
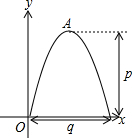 如图,一抛物线桥拱的最高点A到水面的距离为p,在水面上截得的距离为q,如图所示,建立平面直角坐标系.
如图,一抛物线桥拱的最高点A到水面的距离为p,在水面上截得的距离为q,如图所示,建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 课外阅读是提高学生素养的重要途径,某校团委为了解学生课外阅读情况,随机抽查了本校n名学生,统计它们平均每天课外阅读时间t(时),并根据时间t的长短分为A、B、C、D四类,(A)0<t<0.5,(B)0.5≤t<1,(C)1≤t<1.5,(D)t≥1.5,并根据抽查的人数绘制如下统计图.
课外阅读是提高学生素养的重要途径,某校团委为了解学生课外阅读情况,随机抽查了本校n名学生,统计它们平均每天课外阅读时间t(时),并根据时间t的长短分为A、B、C、D四类,(A)0<t<0.5,(B)0.5≤t<1,(C)1≤t<1.5,(D)t≥1.5,并根据抽查的人数绘制如下统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
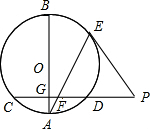 如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com