
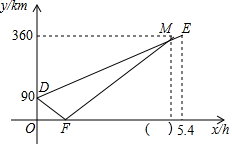
 A,B,C三地在同一条公路上,A地在B,C两地之间,甲、乙两车同时从A地出发匀速行驶,甲车驶向C地,乙车先驶向B地,到达B地后,调头按原速经过A地驶向C地(调头时间忽略不计),到达C地停止行驶,甲车比乙车晚0.4小时到达C地,两车距B地的路程y(km)与行驶时间x(h)之间的函数关系如图所示,请结合图象信息,解答下列问题:
A,B,C三地在同一条公路上,A地在B,C两地之间,甲、乙两车同时从A地出发匀速行驶,甲车驶向C地,乙车先驶向B地,到达B地后,调头按原速经过A地驶向C地(调头时间忽略不计),到达C地停止行驶,甲车比乙车晚0.4小时到达C地,两车距B地的路程y(km)与行驶时间x(h)之间的函数关系如图所示,请结合图象信息,解答下列问题:分析 (1)观察图象找出A、C两地间的距离,再根据速度=路程÷时间,即可求出甲车行驶的速度;由甲车比乙车晚0.4小时到达C地结合甲车5.4小时到达C地,可得出乙车到达C地所用时间;
(2)根据速度=路程÷时间可求出乙车的速度,由时间=路程÷速度可得出点F的横坐标,再根据路程=速度×(时间-1),即可得出线段FM所表示的y与x的函数解析式;
(3)根据路程=速度×时间(路程=90-速度×时间),可得出线段DM(DF)所表示的y与x的函数解析式,分0<x≤1以及1<x<5两种情况,找出关于x的一元一次方程,解之即可得出结论.
解答 解:(1)A、C两地间的距离为360-90=270(km),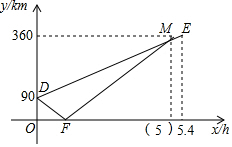
甲车行驶的速度为270÷5.4=50(km/h),
乙车达到C地所用时间为5.4-0.4=5(h).
故答案为:50;5.
(2)乙的速度为(90+360)÷5=90(km/h),
点F的横坐标为90÷90=1.
∴线段FM所表示的y与x的函数解析式为y=90(x-1)=90x-90(1≤x≤5).
(3)线段DE所表示的y与x的函数解析式为y=50x+90(0≤x≤5.4),
线段DF所表示的y与x的函数解析式为y=90-90x(0≤x≤1).
当0<x≤1时,有90-(90-90x)=50x+90-90,
解得:x=0(舍去);
当1<x<5时,有|90x-90-90|=50x+90-90,
解得:x1=$\frac{9}{7}$,x2=$\frac{9}{2}$.
答:在乙车到达C地之前,甲、乙两车出发后$\frac{9}{7}$小时或$\frac{9}{2}$小时与A地路程相等.
点评 本题考查了一次函数的应用以及解含绝对值符号的一元一次方程,解题的关键是:(1)根据数量关系,列式计算;(2)根据数量关系,找出函数解析式;(3)分0<x≤1以及1<x<5两种情况,找出关于x的一元一次方程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
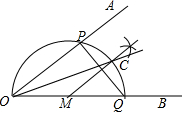 已知∠AOB,作图.
已知∠AOB,作图.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度为别为40公分,50公分,今将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,求隔板抽出后水面静止时,箱内的水面高度为多少公分( )
如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度为别为40公分,50公分,今将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,求隔板抽出后水面静止时,箱内的水面高度为多少公分( )| A. | 43 | B. | 44 | C. | 45 | D. | 46 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
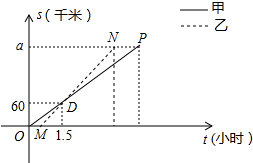 顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1(h)到达B地,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,a表示A、B两地之间的距离.请结合图中的信息解决如下问题:
顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1(h)到达B地,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,a表示A、B两地之间的距离.请结合图中的信息解决如下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com