
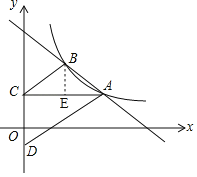
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

【答案】(1) m=4,k=8,n=4;(2)△ABC的面积为4.
【解析】试题分析:(1)由点A的纵坐标为2知OC=2,由OD=![]() OC知OD=1、CD=3,根据△ACD的面积为6求得m=4,将A的坐标代入函数解析式求得k,将点B坐标代入函数解析式求得n;
OC知OD=1、CD=3,根据△ACD的面积为6求得m=4,将A的坐标代入函数解析式求得k,将点B坐标代入函数解析式求得n;
(2)作BE⊥AC,得BE=2,根据三角形面积公式求解可得.
试题解析:(1)∵点A的坐标为(m,2),AC平行于x轴,
∴OC=2,AC⊥y轴,
∵OD=OC,
∴OD=1,
∴CD=3,
∵△ACD的面积为6,
∴![]() CDAC=6,
CDAC=6,
∴AC=4,即m=4,
则点A的坐标为(4,2),将其代入y=![]() 可得k=8,
可得k=8,
∵点B(2,n)在y=![]() 的图象上,
的图象上,
∴n=4;
(2)如图,过点B作BE⊥AC于点E,则BE=2,
∴S△ABC=![]() ACBE=
ACBE=![]() ×4×2=4,
×4×2=4,
即△ABC的面积为4.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
日期x | 1 | 2 | 3 | 4 |
水位y(米) | 20.00 | 20.50 | 21.00 | 21.50 |
(1)请建立该水库水位y与日期x之间的函数模型;
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:①线段是轴对称图形,②成轴对称的两个图形对称点的连线互相平行,③等腰三角形的角平分线就是底边的垂直平分线,④已知两腰就能确定等腰三角形的形状和大小,正确的有( ) .
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,点F,点M都在直线l上,且点E和点F关于点M对称,直线EA与直线OF交于点P.
(Ⅰ)若点M的坐标为(1,﹣1),
①当点F的坐标为(1,1)时,如图,求点P的坐标;
②当点F为直线l上的动点时,记点P(x,y),求y关于x的函数解析式.
(Ⅱ)若点M(1,m),点F(1,t),其中t≠0,过点P作PQ⊥l于点Q,当OQ=PQ时,试用含t的式子表示m.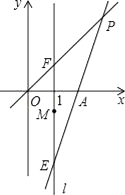
查看答案和解析>>
科目:初中数学 来源: 题型:
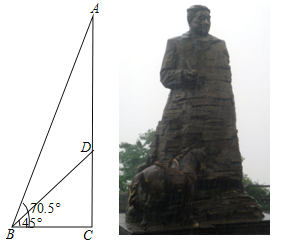
【题目】位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习片段展示:
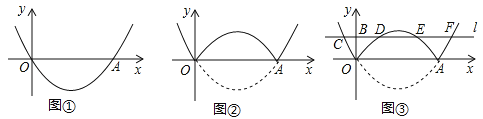
【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣![]() 经过原点O,与x轴的另一个交点为A,则a= .
经过原点O,与x轴的另一个交点为A,则a= .
【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G,如图②.直接写出图象G对应的函数解析式.
【探究】在图②中,过点B(0,1)作直线l平行于x轴,与图象G的交点从左至右依次为点C,D,E,F,如图③.求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围.
【应用】P是图③中图象G上一点,其横坐标为m,连接PD,PE.直接写出△PDE的面积不小于1时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场甲、乙、丙三名业务员5个月的销售额(单位:万元)如下表:
月份销售额人员 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 7.2 | 9.6 | 9.6 | 7.8 | 9.3 |
乙 | 5.8 | 9.7 | 9.8 | 5.8 | 9.9 |
丙 | 4 | 6.2 | 8.5 | 9.9 | 9.9 |
(1)根据上表中的数据,将下表补充完整:
统计值 数值 人员 | 平均数(万元) | 中位数(万元) | 众数(万元) |
甲 | 9.3 | 9.6 | |
乙 | 8.2 | 5.8 | |
丙 | 7.7 | 8.5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.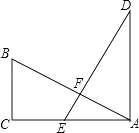
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:![]() =1-
=1- ![]() ,
, ![]() =
= ![]() -
- ![]() ,
, ![]() =
= ![]() -
- ![]() .
.
将以上三个等式的两边分别相加,得:![]() +
+ ![]() +
+ ![]() =1-
=1- ![]() +
+ ![]() -
- ![]() +
+ ![]() -
- ![]() =1-
=1- ![]() =
= ![]() .
.
(1)直接写出计算结果:![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =.
=.
(2)仿照 ![]() =1-
=1- ![]() ,
, ![]() =
= ![]() -
- ![]() ,
, ![]() =
= ![]() -
- ![]() 的形式,猜想并写出:
的形式,猜想并写出: ![]() =.
=.
(3)解方程: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com