
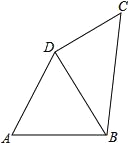
【题目】如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
(1)求∠BDC的度数;
(2)四边形ABCD的面积.
【答案】(1)90°;(2)24+16![]()
【解析】
(1)先根据题意得出△ABD是等边三角形,△BCD是直角三角形,进而可求出∠BDC的度数;
(2)根据四边形周长计算BC,CD,即可求△BCD的面积,正△ABD的面积根据计算公式计算,即可求得四边形ABCD的面积为两个三角形的面积的和.
(1)∵AB=AD=8cm,∠A=60°,∴△ABD是等边三角形.
∵∠ADC=150°,∴∠BDC=150°﹣60°=90°;
(2)∵△ABD为正三角形,AB=8cm,∴其面积为![]() ×
×![]() ×AB×AD=16
×AB×AD=16![]() .
.
∵BC+CD=32﹣8﹣8=16,且BD=8,BD2+CD2=BC2,解得:BC=10,CD=6,∴直角△BCD的面积=![]() ×6×8=24,故四边形ABCD的面积为24+16
×6×8=24,故四边形ABCD的面积为24+16![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. 
(1)求证:△ACD∽△AEC;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4 ![]() ,求△ACE的面积.
,求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形ABC中,D是边BC上的一点,已知AC=5,AD=6,BD=10,CD=5,那么三角形ABC的面积是( )
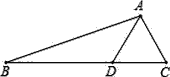
A. 30 B. 36 C. 72 D. 125
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=﹣ ![]() x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.
(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE
(1)请判断:AF与BE的数量关系是 , 位置关系是 .
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予说明
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com