
【题目】(解决问题)已知![]() ,
,![]() ,
,![]() 是同一平面上的三个点,以线段
是同一平面上的三个点,以线段![]() ,
,![]() 为边,分别作正三角形
为边,分别作正三角形![]() 和正三角形
和正三角形![]() ,连接
,连接![]() ,
,![]() .
.
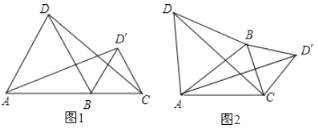
(1)如图1,当点![]() ,
,![]() ,
,![]() 在同一直线上时,线段
在同一直线上时,线段![]() 与
与![]() 的大小关系是__________;
的大小关系是__________;
(2)如图2,当![]() ,
,![]() ,
,![]() 为三角形的顶点时(点
为三角形的顶点时(点![]() ,
,![]() ,
,![]() 不在同一条直线上),判断线段
不在同一条直线上),判断线段![]() 与
与![]() 的大小关系是否发生改变,并说明理由;
的大小关系是否发生改变,并说明理由;
(类比猜想)
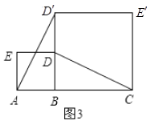
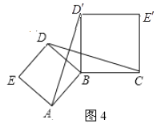
(3)已知![]() ,
,![]() ,
,![]() 是同一平面上的三个点,以线段
是同一平面上的三个点,以线段![]() ,
,![]() 为边,分别作正方形,连接
为边,分别作正方形,连接![]() ,
,![]() ,如图3和图4所示.判断线段
,如图3和图4所示.判断线段![]() 与
与![]() 的大小关系,并在图4(点
的大小关系,并在图4(点![]() ,
,![]() ,
,![]() 不在同一条直线上)中证明你的判断;
不在同一条直线上)中证明你的判断;
(推广应用)(4)上面的这些结论能否推广到任意正多边形(不必证明)?
(5)如图5,![]() 与
与![]() 的大小关系是__________,并写出它们分别在哪两个全等三角形中;
的大小关系是__________,并写出它们分别在哪两个全等三角形中;
(6)请在图6中连接图中两个顶点,构造处一组全等三角形,并写出这两个全等的三角形.

【答案】(1)相等;(2)没有发生变化,理由见解析;(3)![]() =
=![]() ,理由见解析;(4)能推广到任意正多边形;(5)相等;△ABD’≌△DBC;(6)△GAD’≌△BAC.
,理由见解析;(4)能推广到任意正多边形;(5)相等;△ABD’≌△DBC;(6)△GAD’≌△BAC.
【解析】
(1)根据正三角形的性质证明△ABD’≌△DBC,即可求解;
(2)同理证明△ABD’≌△DBC,即可求解;
(3)根据正方形的性质同理证明△ABD’≌△DBC,即可求解;
(4)根据题意及图形的特点可知这些结论能否推广到任意正多边形;
(5)根据正五边形的性质同理证明△ABD’≌△DBC,即可求解;
(6)连接GD’,证明△ABC≌△AGD’即可求解.
(1)∵△ABD、△BCD’是等边三角形,
∴AB=BD,BD’=BC, ![]()
∵![]() ,
,![]()
∴![]()
∴△ABD’≌△DBC(SAS)
∴![]() =
=![]()
故答案为:相等;
(2)线段![]() 与
与![]() 的大小关系没有改变,理由如下:
的大小关系没有改变,理由如下:
∵△ABD、△BCD’是等边三角形,
∴AB=BD,BD’=BC, ![]()
∵![]() ,
,![]()
∴![]()
∴△ABD’≌△DBC(SAS)
∴![]() =
=![]()
(3)在如图3和图4.判断线段![]() 与
与![]() 的大小关系为相等,理由如下:
的大小关系为相等,理由如下:
∵四边形ABDE、四边形BCD’E’是正方形,
∴AB=BD,BD’=BC, ![]()
∵![]() ,
,![]()
∴![]()
∴△ABD’≌△DBC(SAS)
∴![]() =
=![]()
故线段![]() 与
与![]() 的大小关系为相等;
的大小关系为相等;
(4)根据题意及图形的特点同理可得△ABD’≌△DBC,则![]() =
=![]()
故线段![]() 与
与![]() 的大小关系为相等,能推广到任意正多边形;
的大小关系为相等,能推广到任意正多边形;
(5)∵五边形ABDEF、五边形BCF’E’ D’是正方形,
∴AB=BD,BD’=BC, ![]()
∵![]() ,
,![]()
∴![]()
∴△ABD’≌△DBC(SAS)
∴![]() =
=![]()
故答案为:相等;△ABD’≌△DBC;
(6)如图,连接GD’,
∵六边形ABDEFG、六边形ACG’F’E’ D’是正方形,
∴AB=AG,AD’=AC, ![]()
∵![]() ,
,![]()
∴![]()
∴△GAD’≌△BAC(SAS)
故答案为△GAD’≌△BAC.


科目:初中数学 来源: 题型:
【题目】每年“双11”天猫商城都会推出各种优惠活动进行促销,今年,王阿姨在“双11”到来之前准备在两家天猫店铺中选择一家购买原价均为1000元/条的被子2条和原价均为600元/个的颈椎枕若干个,已知两家店铺在活动期间分别给予以下优惠:
![]() 店铺:“双11”当天购买所有商品可以享受8折优惠;
店铺:“双11”当天购买所有商品可以享受8折优惠;
![]() 店铺:买2条被子,可赠送1个颈椎枕,同时“双11”当天下单,还可立减160元;
店铺:买2条被子,可赠送1个颈椎枕,同时“双11”当天下单,还可立减160元;
设购买颈椎枕![]() (个),若王阿姨在“双11”当天下单,
(个),若王阿姨在“双11”当天下单,![]() 两个店铺优惠后所付金额分别为
两个店铺优惠后所付金额分别为![]() (元)、
(元)、![]() (元).
(元).
(1)试分别表示![]() 、
、![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)王阿姨准备在“双11”当天购买4个颈椎枕,通过计算说明在哪家店铺购买更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
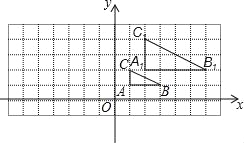
【题目】如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1.
(1)△A1B1C1与△ABC的位似比是 ;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)设点P(a,b)为△ABC内一点,则依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
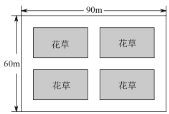
【题目】成都市中心城区“小游园,微绿地”规划已经实施,武侯区某街道有一块矩形空地进入规划试点.如图,已知该矩形空地长为![]() ,宽为
,宽为![]() ,按照规划将预留总面积为
,按照规划将预留总面积为![]() 的四个小矩形区域(阴影部分)种植花草,并在花草周围修建三条横向通道和三条纵向通道,各通道的宽度相等.
的四个小矩形区域(阴影部分)种植花草,并在花草周围修建三条横向通道和三条纵向通道,各通道的宽度相等.
(1)求各通道的宽度;
(2)现有一工程队承接了对这![]() 的区域(阴影部分)进行种植花草的绿化任务,该工程队先按照原计划进行施工,在完成了
的区域(阴影部分)进行种植花草的绿化任务,该工程队先按照原计划进行施工,在完成了![]() 的绿化任务后,将工作效率提高
的绿化任务后,将工作效率提高![]() ,结果提前
,结果提前![]() 天完成任务,求该工程队原计划每天完成多少平方米的绿化任务?
天完成任务,求该工程队原计划每天完成多少平方米的绿化任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽学完统计知识后,随机调查了她所在辖区若干名居民的年龄,并绘制成如下统计图.
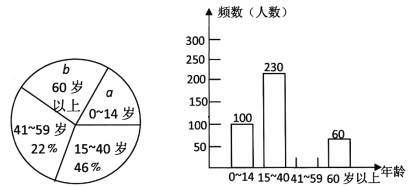
请根据统计图提供的信息,解答下列问题
(1)小丽共调查了 名居民的年龄,扇形统计图中a= %,b= %;
(2)补全条形统计图;
(3)若该辖区0~14岁的居民约有3500人,请估计年龄在60岁以上的居民人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
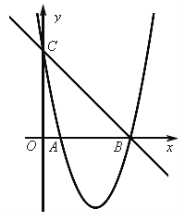
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,两直角边AC=8cm,BC=6cm.
(1)作∠BAC的平分线AD交BC于点D;(尺规作图,不写作法,保留作图痕迹)
(2)计算△ABD的面积.
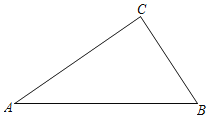
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD中,对角线AC、BD交于点O,过O点的两直线OE、OF互相垂直,分别交AB、BC于E、F,连接EF.
(1)求证:OE=OF;
(2)若AE=4,CF=3,求EF的长;
(3)若AB=8cm,请你计算四边形OEBF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com