
【题目】如图,点E、F分别是ABCD的边BC、AD上的点,且BE=DF.

(1)试判断四边形AECF的形状;
(2)若AE=BE,∠BAC=90°,求证:四边形AECF是菱形.
【答案】(1)四边形AECF为平行四边形;(2)见解析
【解析】
试题分析:(1)四边形AECF为平行四边形.通过平行四边形的判定定理“有一组对边平行且相等的四边形是平行四边形”得出结论:四边形AECF为平行四边形.
(2)根据直角△BAC中角与边间的关系证得△AEC是等腰三角形,即平行四边形AECF的邻边AE=EC,易证四边形AECF是菱形.
(1)解:四边形AECF为平行四边形.
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
又∵BE=DF,∴AF=CE,
∴四边形AECF为平行四边形;
(2)证明:∵AE=BE,∴∠B=∠BAE,
又∵∠BAC=90°,∴∠B+∠BCA=90°,∠CAE+∠BAE=90°,
∴∠BCA=∠CAE,
∴AE=CE,
又∵四边形AECF为平行四边形,
∴四边形AECF是菱形.


科目:初中数学 来源: 题型:
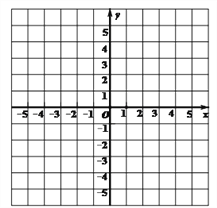
【题目】在如图的直角坐标系中,画出函数y=-2x+3的图象,并结合图象回答下列问题:
(1)y的值随x值的增大而 (填“增大”或“减小”);
(2)图象与x轴的交点坐标是 ;图象与y轴的交点坐标是 ;
(3)当x 时,y <0 ;
(4)直线y=-2x+3与两坐标轴所围成的三角形的面积是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
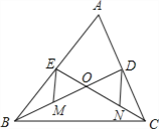
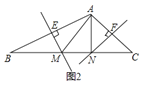
【题目】如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.
(1)求证:MD和NE互相平分;
(2)若BD⊥AC,EM=2![]() ,OD+CD=7,求△OCB的面积.
,OD+CD=7,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数y= ![]() (x﹣6)2+3的图象,下列叙述错误的是( )
(x﹣6)2+3的图象,下列叙述错误的是( )
A.图象是抛物线,开口向上
B.对称轴为直线x=6
C.顶点是图象的最高点,坐标为(6,3)
D.当x<6时,y随x的增大而减小;当x>6时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为2,AB∥x轴,AD∥y轴,顶点A恰好落在双曲线y= ![]() 上,边CD,BC分别交双曲线于E,F两点,若线段AE过原点,则EF的长为( )
上,边CD,BC分别交双曲线于E,F两点,若线段AE过原点,则EF的长为( ) 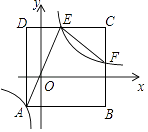
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
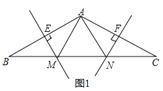
【题目】![]() 如图
如图![]() 所示,在
所示,在![]() 中,
中,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() 的周长
的周长![]() ;21.
;21.
![]() 如图
如图![]() 所示,在
所示,在![]() 中,若
中,若![]() ,
,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,试判断
,试判断![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
![]() 如图
如图![]() 所示,在
所示,在![]() 中,若
中,若![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专买店销售A,B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的件价各为多少万元;
每辆A型车和B型车的售价分别是x万元,y万元.
根据题意,列方程组
解这个方程组,得x= ,y=
答: .
(2)有一家公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不超过130万元,求这次购进B型车最多几辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,a是
,a是![]() 的立方根,方程
的立方根,方程![]() 是关于x,y的二元一次方程,d为不等式组
是关于x,y的二元一次方程,d为不等式组![]() 的最大整数解.
的最大整数解.
![]() 求点A、B、C的坐标;
求点A、B、C的坐标;
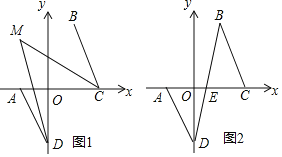
![]() 如图1,若D为y轴负半轴上的一个动点,当
如图1,若D为y轴负半轴上的一个动点,当![]() 时,
时,![]() 与
与![]() 的平分线交于M点,求
的平分线交于M点,求![]() 的度数;
的度数;
![]() 如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使
如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使![]() ?若存在,请求出D的纵坐标
?若存在,请求出D的纵坐标![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com