

���� ��1������SAS����֤����BED�ա�CAD��
��2���ڡ�ABE�������߹�ϵ�������ɽ����
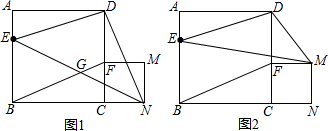
������⣺�ӳ�GE��CB���ӳ�����M��ֻҪ֤����AEG�ա�BEM���Ƴ�AG=CM=2���ٸ����߶εĴ�ֱƽ���ߵ����ʣ����ɽ�����⣮
��� �⣺��1����ͼ2�У��ӳ�AD��E��ʹDE=AD������BE��
�ڡ�BED�͡�CAD�У�
$\left\{\begin{array}{l}{BD=CD}\\{��BDE=��ADC}\\{ED=AD}\end{array}\right.$��
���BED�ա�CAD��SAS����
��2���ߡ�BED�ա�CAD��
��BE=AC=5����AB=7��
��2��AE��12��
��2��2AD��12��
��1��AD��6��
�ʴ𰸷ֱ�ΪSAS��1��AD��6��
������⣺��ͼ3�У�
�⣺�ӳ�GE��CB���ӳ�����M��
���ı���ABCD�������Σ�
��AD��CM��
���AGE=��M��
�ڡ�AEG�͡�BEM�У�
$\left\{\begin{array}{l}{��AGE=��M}\\{��AEG=��MEB}\\{AE=BE}\end{array}\right.$��
���AEG�ա�BEM��
��GE=EM��AG=BM=2��
��EF��MG��
��FG=FM��
��BF=4��
��MF=BF+BM=2+4=6��
��GF=FM=6��
���� ���⿼�������ε����ʡ������ε����ߡ�ȫ�������ε��ж������ʡ����������߹�ϵ������֪ʶ������Ĺؼ���ѧ�����Ӹ����ߣ�����ȫ�������ν�����⣬�����п��������ͣ�


 �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д� �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ������a��b�������ϵ�λ����ͼ��ʾ�������н����У�
������a��b�������ϵ�λ����ͼ��ʾ�������н����У�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -7 | B�� | 5 | C�� | -5 | D�� | -13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
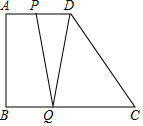 ��֪��������ABCD�У�AD��BC����ABC=90�㣬AD=12��BC=24������P��AD����ӵ�A������D����ÿ��1����λ���ٶ��˶�������Q�ӵ�C��������CB������ÿ��2����λ���ٶ��˶���P��Qͬʱ����������Pֹͣ�˶�ʱ����QҲ��ֹ֮ͣ�˶�������PQ��DQ�����P�˶���ʱ��Ϊx�룬�������xΪ��ֵʱ����PDQ�ա�CQD��
��֪��������ABCD�У�AD��BC����ABC=90�㣬AD=12��BC=24������P��AD����ӵ�A������D����ÿ��1����λ���ٶ��˶�������Q�ӵ�C��������CB������ÿ��2����λ���ٶ��˶���P��Qͬʱ����������Pֹͣ�˶�ʱ����QҲ��ֹ֮ͣ�˶�������PQ��DQ�����P�˶���ʱ��Ϊx�룬�������xΪ��ֵʱ����PDQ�ա�CQD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����������ȵ�ʵ���� | B�� | ��������ȵ�ʵ���� | ||
| C�� | ֻ��һ��ʵ���� | D�� | û��ʵ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com