
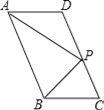
【题目】如图,在ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是_______.
【答案】24
【解析】试题分析:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=![]() (∠DAB+∠CBA)=90°,
(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA,
∴∠DAP=∠DPA,
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP=![]() =6,
=6,
,∴△APB的周长=6+8+10=24;
故答案为:24.


 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
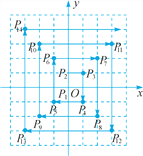
【题目】如图,在平面直角坐标系中,每个最小方格的边长均为1个单位,P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:点P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2),….根据这个规律,求点P2018的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
(1)求此抛物线的函数表达式;
(2)设E是y轴右侧抛物线上异于点B的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH.则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)在抛物线上是否存在异于B、C的点M,使△MBC中BC边上的高为 ![]() ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某学校在“国学经典”中新建了一座吴玉章雕塑,小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据: ![]() ≈1.7)
≈1.7)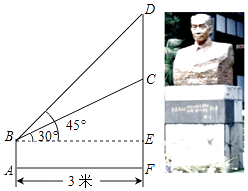
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90,当点D在线段BC上时(与点B不重合),如图2,线段CF,BD所在直线位置关系为 ,数量关系为 .
(2)如果AB=AC,∠BAC=90,当点D在线段BC的延长线时,如图3,(1)中的结论是否仍然成立,并说明理由。
(3)如果AB=AC,∠BAC是钝角,点D在线段BC上,当∠ABC满足什么条件时,CF⊥BC(点C、F不重合)画出图形,并说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com