
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
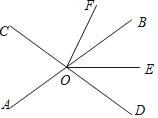
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)若|∠AOC﹣∠BOF|=α°,请直接写出∠AOC和∠BOF的度数.(用含的代数式表示)
【答案】(1)∠BOF=33°;(2)∠AOC=72°;(3) ∠AOC=2x=(![]() )°﹣
)°﹣![]() α°,∠BOF=(
α°,∠BOF=(![]() )°+
)°+![]() α°.
α°.
【解析】试题分析:
(1)由∠AOC=76°易得∠BOD=76°,结合OE平分∠BOD可得∠DOE=∠BOE=38°,由此可得∠COE=180°-38°=142°,结合OF平分∠COE可得∠EOF=71°,最后由∠BOF=∠EOF-∠BOE即可求得∠BOF的度数;
(2)设∠BOE=x,由OE平分∠BOD,∠AOC=∠BOD可得∠DOE=∠BOE=x,∠AOC=2x,结合∠BOF=36°,OF平均∠EOF可得∠COF=∠EOF=x+36°,最后由∠AOC+∠COF+∠BOF=180°即可列出关于x的方程,解方程求得x的值即可求得∠AOC的度数;
(3)设∠BOE=x,则由已知条件易得∠AOC=2x,∠BOF=90°-![]() x,这样结合|∠AOC﹣∠BOF|=α°即可列出关于x的方程,解方程求得x的值即可求得∠AOC和∠BOF的值.
x,这样结合|∠AOC﹣∠BOF|=α°即可列出关于x的方程,解方程求得x的值即可求得∠AOC和∠BOF的值.
试题解析:
(1)∵∠BOD=∠AOC=76°,
又∵OE平分∠BOD,
∴∠DOE=![]() ∠BOD=
∠BOD=![]() ×76°=38°.
×76°=38°.
∴∠COE=180°﹣∠DOE=180°﹣38°=142°,
∵OF平分∠COE,
∴∠EOF=![]() ∠COE=
∠COE=![]() ×142°=71°,
×142°=71°,
∴∠BOF=∠EOF﹣∠BOE=71°﹣38°=33°.
(2)∵OE平分∠BOD,OF平分∠COE,
∴∠BOE=∠EOD,∠COF=∠FOE,
∴设∠BOE=x,则∠DOE=x,
故∠COA=2x,∠EOF=∠COF=x+36°,
则∠AOC+∠COF+∠BOF=2x+x+36°+36°=180°,
解得:x=36°,
故∠AOC=72°.
(3)设∠BOE=x,
∵OE平分∠BOD,∠BOD=∠AOC,
∴∠DOE=x,∠COA=2x,
∴∠BOC=180°-2x,
∴∠COE=180°-x,
∵OF平分∠COE,
∴∠EOF=90°-![]() x,
x,
∴∠BOF=90°﹣![]() x,
x,
∵|∠AOC﹣∠BOF|=α°,
∴|2x﹣(90°﹣![]() x)|=α°,
x)|=α°,
解得:x=(![]() )°+
)°+![]() α°或x=(
α°或x=(![]() )°﹣
)°﹣![]() α°,
α°,
当x=(![]() )°+
)°+![]() α°时,
α°时,
∠AOC=2x=(![]() )°+
)°+![]() α°,
α°,
∠BOF=90°﹣![]() x=(
x=(![]() )°﹣
)°﹣![]() α°;
α°;
当x=(![]() )°﹣
)°﹣![]() α°时,
α°时,
∠AOC=2x=(![]() )°﹣
)°﹣![]() α°,
α°,
∠BOF=90°﹣![]() x=(
x=(![]() )°+
)°+![]() α°.
α°.


科目:初中数学 来源: 题型:
【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,AB=BC=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,点D的对应点为D′,连接D′B.若△D′BC为等边三角形,则DE=____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为体现社会对教师的尊重,教师节这天上午,出租车司机小王在东西走向的公路上免费接送老师.如果规定向东为正,向西为负,出租车的行程如下.(单位:千米)+15,﹣4,+13,﹣10,﹣12,+3,﹣13,﹣17
(1)当最后一名老师到达目的地时,小王距离开始接送第一位老师之前的地点的距离是多少?
(2)若出租车的耗油量为0.4升/千米,这天上午出租车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.
(1)若AB=10cm,则MN= cm;
(2)若AC=3cm,CP=1cm,求线段PN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在数轴上对应的数为a,点B在数轴上对应的数为b,且|a+3|+|b-2|=0,A,B 之间的距离记为|AB|.请回答问题:
(1)直接写出a,b, |AB|的值. a= ,b = , |AB|= ;
(2)设点P在数轴上对应的数为x,当|PA|-|PB|=2时,求x的值;
(3)若点P在点A的左侧,M、N分别是PA、PB的中点.当点P在点A的左侧移动时,式子|PN|-|PM|的值是否发生改变?若不变,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图.则在字母L,K,C的投影中,与字母N属同一种投影的有( ) 
A.L,K
B.C
C.K
D.L,K,C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com