
【题目】已知:点P在△ABC内,且满足∠APB=∠APC(如下图),∠APB+∠BAC=180°,
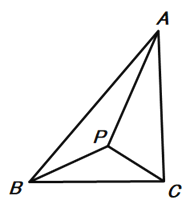
(1)求证:△PAB∽△PCA:
(2)如下图,如果∠APB=120°,∠ABC=90°求![]() 的值;
的值;
(3)如图,当∠BAC=45°,△ABC为等腰三角形时,求tan∠PBC的值.
【答案】(1)见解析;(2)4;(3)2或![]() 或1
或1
【解析】
(1)由已知和等量代换得∠PBA=∠PAC,再根据∠APB=∠APC可证明△PAB∽△PCA
(2)由△PAB∽△PCA可得![]() ,通过变形得到
,通过变形得到![]() ,再利用∠APB=120°,∠ABC=90°求出
,再利用∠APB=120°,∠ABC=90°求出![]() ,则可得出
,则可得出![]() 的值.
的值.
(3)当∠BAC=45°时,可以推出tan∠BPC=![]() ,△ABC为等腰三角形,分BA=BC,CA=CB ,AB=AC三种情况,分情况讨论即可.
,△ABC为等腰三角形,分BA=BC,CA=CB ,AB=AC三种情况,分情况讨论即可.
(1)∵∠APB+∠PBA+∠PBA=180°,∠APB+∠BAC=180°
∴∠BAC=∠PAB+∠PBA
∴∠PBA=∠PAC
∵∠APB=∠APC
∴△PAB∽△PCA
(2)
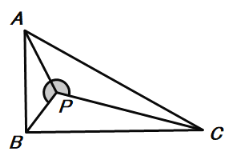
∵△PAB∽△PCA
∴![]()
∴![]()
∵∠APB=120°
∴∠BAC=60°
∵∠ABC=90°
∴![]()
∴![]()
(3)



∵∠BAC=45°
∴∠APB=135°=∠APC
∴∠BPC=90°
tan∠BPC=![]()
∵∠BAC=45°,△ABC是等腰三角形
当BA=BC时,由勾股定理可得![]() ,tan∠BPC=
,tan∠BPC=![]()
当CA=CB时,由勾股定理可得![]() ,tan∠BPC=
,tan∠BPC=![]()
当AB=AC 时,tan∠BPC=![]()
综上所述,tan∠PBC=2或![]() 或1
或1


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线![]() 经过点A,B.
经过点A,B.
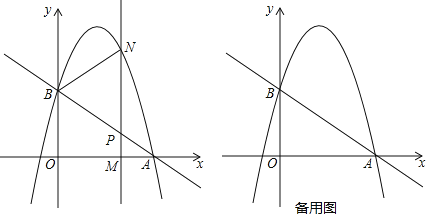
(1)求点B的坐标和抛物线的解析式;
(2)设点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①求PN的最大值;
②若以B,P,N为顶点的三角形与△APM相似,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程
(1)(x﹣8)(x﹣1)=﹣12;
(2)3(x﹣5)2=2(5﹣x).
(3)y2-7y+6=0;
(4)2x2-4x-3=0;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2![]() .
.
(1)如图1,将△DEC沿射线EC方向平移,得到△D′E′C′,边D′E′与AC的交点为M,边C′D′与∠ACC′的角平分线交于点N,当CC′多大时,四边形MCND′为菱形?并说明理由.
(2)如图2,将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD′、BE′.边D′E′的中点为P.
①在旋转过程中,AD′和BE′有怎样的数量关系?并说明理由;
②连接AP,当AP最大时,求AD′的值.(结果保留根号)
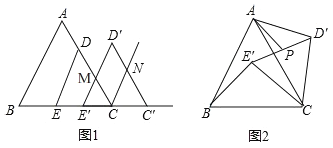
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣4ax+3a.
(1)若a=1,则函数y的最小值为_______.
(2)当1≤x≤4时,y的最大值是4,则a的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,泰兴市教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
⑴在这次调查中一共调查了多少名学生?
⑵求户外活动时间为1.5小时的人数,并补全频数分布直方图;
⑶求表示户外活动时间 1小时的扇形圆心角的度数;
⑷本次调查中,学生参加户外活动的平均时间是否符合要求?户外活动时间的众数和中位数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴相交于A(3,0)、B两点,与y轴交于点C(0,3),点B在x轴的负半轴上,且
与x轴相交于A(3,0)、B两点,与y轴交于点C(0,3),点B在x轴的负半轴上,且![]() .
.
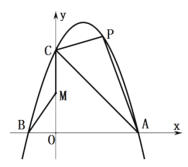

(1)求抛物线的函数关系式;
(2)若P是抛物线上且位于直线![]() 上方的一动点,求
上方的一动点,求![]() 的面积的最大值及此时点P的坐标;
的面积的最大值及此时点P的坐标;
(3)在线段![]() 上是否存在一点M,使
上是否存在一点M,使![]() 的值最小?若存在,请求出这个最小值及对应的M点的坐标;若不存在,请说明理由.
的值最小?若存在,请求出这个最小值及对应的M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
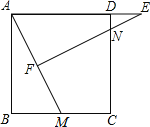
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com