
分析 (1)根据待定系数法,可得答案;
(2)根据定点公式,可得(1,-1),根据平移规律,可得答案.
解答 解法(1):将P(-3,m),Q(1,m)代入y=2x2+bx+1中得:
$\left\{\begin{array}{l}{m=18-3b+1}\\{m=2+b+1}\end{array}\right.$,
19-3b=3+b
解得b=4
(2):由(1)知:b=4
∴抛物线为:y=2x2+4x+1
=2(x+1)2-1
其点为:(1,-1)
向上平移k个单位后,顶点为(1,-1+k).
又∵此顶在x轴上
∴-1+k=0.
即:k=1.
点评 本题考查了二次函数图象与几何变换,熟练掌握平移的规律:左加右减,上加下减是解题关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
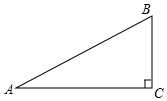 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
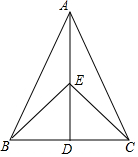 如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )
如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )| A. | △ABD≌△ACE | B. | △ABE≌△ACE | C. | △BDE≌△CDE | D. | △ABD≌△ACD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
| 钱数变化 | +300 | +220 | -150 | -100 | +330 | +200 | +280 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
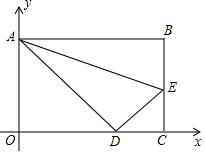 如图,在矩形OABC中,点C在x轴上,点A在y轴上,且OA,OC的长分别是一元二次方程x2-18x+80=0的两个根(OA<OC),点E在BC上,将△ABE沿AE折叠,使点B落在OC上.
如图,在矩形OABC中,点C在x轴上,点A在y轴上,且OA,OC的长分别是一元二次方程x2-18x+80=0的两个根(OA<OC),点E在BC上,将△ABE沿AE折叠,使点B落在OC上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com