
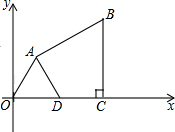
 如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC于点C,点A的坐标为(2,2$\sqrt{3}$),AB=4$\sqrt{3}$,∠B=60°,点D是线段OC上一点,且OD=4,连接AD.
如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC于点C,点A的坐标为(2,2$\sqrt{3}$),AB=4$\sqrt{3}$,∠B=60°,点D是线段OC上一点,且OD=4,连接AD.分析 (1)过点A作AM⊥x轴于点M,根据已知条件,依据三角函数求得∠AOM=60°,根据勾股定理求得OA=4,即可求得.
(2)过点A作AN⊥BC于点N,则四边形AMCN是矩形,在Rt△ABN中,根据三角函数求得AN、BN的值,从而求得OC、BC的长,得出点B的坐标.
(3)利用等腰三角形的特征,分三种情况探讨:OB=OP,PO=PB,BO=BP,进一步综合得出答案即可.
解答 解:(1)如图2,证明:过点A作AM⊥x轴于点M,
∵点A的坐标为(2,2$\sqrt{3}$),
∴OM=2,AM=2$\sqrt{3}$,
∴在Rt△AOM中,tan∠AOM=$\frac{AM}{OM}$=$\sqrt{3}$,
∴∠AOM=60°,
由勾股定理得,OA=$\sqrt{O{M}^{2}+A{M}^{2}}$=4,
∵OD=4,
∴OA=OD,
∴△AOD是等边三角形.
(2)如图2,过点A作AN⊥BC于点N,
∵BC⊥OC,AM⊥x轴,
∴∠BCM=∠CMA=∠ANC=90°
∴四边形ANCM为矩形,
∴AN=MC,AM=NC,
∵∠B=60°,AB=4$\sqrt{3}$,
∴在Rt△ABN中,
AN=AB•sinB=4$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=6,
BN=AB•cosB=4$\sqrt{3}$×$\frac{1}{2}$=2$\sqrt{3}$,
∴AN=MC=6,CN=AM=2$\sqrt{3}$,
∴OC=OM+MC=2+6=8,
BC=BN+CN=2$\sqrt{3}$+2$\sqrt{3}$=4$\sqrt{3}$,
∴点B的坐标为(8,4$\sqrt{3}$).
(3)如图,
连接OB,则OB=$\sqrt{64+48}$=4$\sqrt{7}$,
当OB=OP,则P1(4$\sqrt{7}$,0),P2(-4$\sqrt{7}$,0)满足条件,
作OB的垂直平分线交x轴于P3,则P3满足条件,设P3(x,0),则x2=(8-x)2+(4$\sqrt{3}$)2,x=7,P3(7,0);
O关于BC的对称点P4(16,0)也满足条件
所以在x轴上求一点P,使△OBP为等腰三角形的点有4个P1(4$\sqrt{7}$,0),P2(-4$\sqrt{7}$,0),P3(7,0),P4(16,0).
点评 本题考查了等边三角形的判定与性质,等腰三角形的性质,锐角三角函数的应用以及勾股定理的应用,注意分类讨论思想的渗透.


科目:初中数学 来源: 题型:选择题
| A. | 购买一张彩票,中奖 | |
| B. | 一个袋中只装有2个黑球,从中摸出一个球是黑球 | |
| C. | 抛掷一枚硬币,正面向上 | |
| D. | 打开电视,正在播放广告 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是某班对40名学生上学出行方式调查的扇形统计图,问:
如图是某班对40名学生上学出行方式调查的扇形统计图,问:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )| A. | 1 | B. | 1+$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在Rt△ABC中,∠C=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交BC于F.
在Rt△ABC中,∠C=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 没有水分,种子发芽 | B. | 367人中至少有2人的生日相同 | ||
| C. | 三角形的内角和是180° | D. | 小华一出门上学,天就下雨 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com