
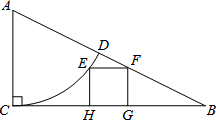
 如图,Rt△ABC中,∠ACB=90°,AC=5,CB=10.以点A为圆心,AC长为半径的弧CD交AB于点D,点E是弧CD上任意一点,EH⊥BC于点H,以EH为边长作正方形EHGF,点F在AB边上,则S正方形EFGH=4.
如图,Rt△ABC中,∠ACB=90°,AC=5,CB=10.以点A为圆心,AC长为半径的弧CD交AB于点D,点E是弧CD上任意一点,EH⊥BC于点H,以EH为边长作正方形EHGF,点F在AB边上,则S正方形EFGH=4. 分析 延长线段FE交线段AC与点M,连接AE,设正方形EHGF的边长为x,用x表示出ME和AM,在直角三角形AME中,由勾股定理即可解得x的值,从而得出正方形EHGF的面积.
解答 解:延长线段FE交线段AC与点M,连接AE,则AE=AC=5,如下图.
设正方形EHGF的边长为x.
在Rt△ABC中,∠ACB=90°,AC=5,CB=10,
tan∠ABC=$\frac{AC}{BC}$=$\frac{1}{2}$.
BG=$\frac{FG}{tan∠ABC}$=$\frac{x}{\frac{1}{2}}$=2x.
∵MF∥BC,AC∥EH,∠ACB=90°,
∴四边形CHEM为长方形,
∴ME=CH,MC=EH,EM⊥AC.
ME=CH=BC-BG-HG=10-2x-x=10-3x,AM=AC-MC=AC-EH=5-x.
在直角△AME中,由勾股定理可得:
AE2=AM2+ME2,即52=(10-3x)2+(5-x)2,
整理,得x2-7x+10=10,
解得x=2,x=5.
∵CH=10-3x>0,
∴x=5舍去.
S正方形EFGH=x2=22=4.
故答案为:4.
点评 本题考查了正方形的性质以及三角函数中的正切,解题的关键是:设正方形EHGF的边长为x,用x表示出ME和AM,在直角三角形AME中,由勾股定理得出关于x的方程.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
 如图,某数学学习兴趣小组为了测量树AB的度数,他们测得此树在阳光下的影子BC的长为9m,在相同时刻,他们还测得小亮在阳光下的影长为1.5m,已知小亮的身高为1.8m,则树AB的高为( )
如图,某数学学习兴趣小组为了测量树AB的度数,他们测得此树在阳光下的影子BC的长为9m,在相同时刻,他们还测得小亮在阳光下的影长为1.5m,已知小亮的身高为1.8m,则树AB的高为( )| A. | 10.8m | B. | 9m | C. | 7.5m | D. | 0.3m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )
如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )| A. | $5\sqrt{3}$米 | B. | 10米 | C. | 15米 | D. | 10$\sqrt{3}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D,BE平分AC,则DE=$\frac{\sqrt{5}-2}{2}$.
如图,在△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D,BE平分AC,则DE=$\frac{\sqrt{5}-2}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数y=-x2-(2m+2)x-m2-4m+3(m为非负整数)与x轴交于A、B两点,与y轴交于C点.
如图,二次函数y=-x2-(2m+2)x-m2-4m+3(m为非负整数)与x轴交于A、B两点,与y轴交于C点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,图中的函数是有界函数,其边界是1.
对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,图中的函数是有界函数,其边界是1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且∠BDA=90°,猜想线段BF、FC的数量关系,并说明理由.
如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且∠BDA=90°,猜想线段BF、FC的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com