
如果一条抛物线 与
与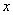 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶 点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶 点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是 三角形;
(2)若抛物线 的“抛物线三角形”是直角三角形,求
的“抛物线三角形”是直角三角形,求 的值;
的值;
(3)若抛物线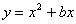 与x轴交与原点O和点B,抛物线的顶点坐标为A,△
与x轴交与原点O和点B,抛物线的顶点坐标为A,△ 是的“抛物线三角形”,是否存在以原点
是的“抛物线三角形”,是否存在以原点 为对称中心的矩形
为对称中心的矩形 ?若存在,求出过
?若存在,求出过 三点的抛物线的表达式;若不存在,说明理由.
三点的抛物线的表达式;若不存在,说明理由.
(1)“抛物线三角形”一定是 等腰 三角形; ……………………1分
(2)(图略)
∵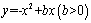 的“抛物线三角形”是直角三角形,
的“抛物线三角形”是直角三角形,
∴此“物线三角形”是等腰直角三角形,抛物线的顶点坐标为(b,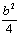 ),
),
把y=0代入得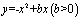 解得x=0或b
解得x=0或b
根据题意得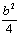 =
=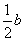
∴b=0或2(0舍去)
∴b=2 ……………………3分
(3)存在.
当b<0时,作AH⊥OB于H点,如图,
把y=0代入y=x2+bx得解得x1=0,x2=-b′,
∴B点坐标为(-b′,0),
∴A点坐标为(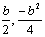 )
)
∵矩形ABCD以原点O为对称中心,
∴OA=OB=OC=OD,
∴△OAB为等边三角形,
∴AH=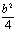
解得b1′=0,b2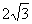
∴A点坐标为( ,-3),B点坐标为(
,-3),B点坐标为(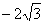 ,0)
,0)
∴C点坐标为(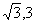 ),D点坐标为(
),D点坐标为(
设过O、C、D三点的抛物线的解析式为y=ax(x-2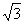 ),
),
把C(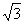 ,3)代入得a=-1,
,3)代入得a=-1,
∴所求抛物线的表达式为y=-x2+2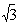
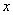 ……………………5分
……………………5分
同理,当b>0时,y=-x2-2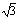
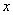 ……………………3分
……………………3分


科目:初中数学 来源: 题型:
某校课程安排中,各班每天下午安排三节课.
(1)某班级星期一下午安排了数学、美术、音乐课各一节,通过画树状图求出把数学课安排在最后一节的概率;
(2)某天下午,初三(1)班安排了数学、社会、音乐课各一节,初三(2)班安排了数学、美术、体育课各一节.已知这两个班的数学课有同一个老师担任,其他课由另外四位老师担任. 通过画树状图或列表格求这两个班数学课不相冲突的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
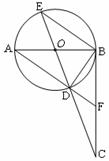
如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.则下列结论正确的有( )
①∠CBD=∠CEB; ② 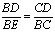 ; ③点F是BC的中点;④若
; ③点F是BC的中点;④若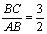 , tanE=
, tanE=
A. ①② B. ③④ C. ①②④ D.①②③
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某市拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A,B,C的位置如图,请利用尺规作图找出音乐喷泉M的位置(要求:不写已知、求作、作法和结论,保留作图痕迹);连结AM、CM,则AM CM。(请在横线上选择填入<,>或=)

查看答案和解析>>
科目:初中数学 来源: 题型:
在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、双曲线、圆,在看不见图形的情况下随机摸出1张,这张卡片上的图形既是中心对称图形又是轴对称图形的概率是( )
A.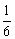 B.
B.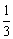 C.
C.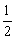 D.
D.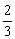
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值。
对于任意正实数a、b,可作如下变形a+b=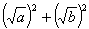 =
=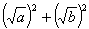 -
-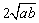 +
+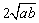 =
=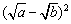 +
+ 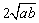 ,
,
又∵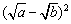 ≥0, ∴
≥0, ∴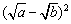 +
+ 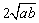 ≥0+
≥0+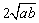 ,即
,即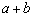 ≥
≥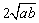 .
.
(1)根据上述内容,回答下列问题:在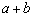 ≥
≥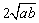 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥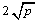 ,当且仅当a、b满足 时,a+b有最小值
,当且仅当a、b满足 时,a+b有最小值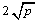 .
.
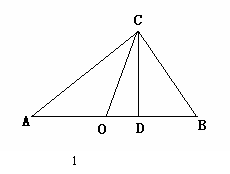
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a,DB=2b, 试根据图形验证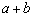 ≥
≥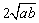 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.
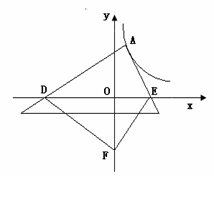
(3)探索应用:如图2,已知A为反比例函数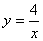 的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com