
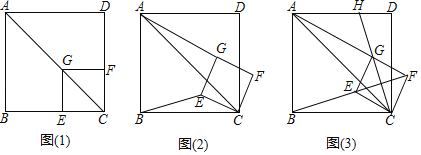
【题目】如图(1),已知点![]() 在止方形
在止方形![]() 的对角线
的对角线![]() 上,
上,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,垂足为
,垂足为![]() .
.
(1)求证:四边形![]() 是正方形并直接写出
是正方形并直接写出![]() 的值.
的值.
(2)将正方形![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() ,如图(2)所小,试探究
,如图(2)所小,试探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)正方形![]() 在旋转过程中,当
在旋转过程中,当![]() ,
,![]() ,
,![]() ,三点在一条直线上时,如图(3)所示,延长
,三点在一条直线上时,如图(3)所示,延长![]() 交
交![]() 于点
于点![]() .若
.若![]() ,
,![]() ,求
,求![]() 的长.
的长.
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+4x-1与y轴交于点C,CD∥x轴交抛物线于另一点D,AB∥x轴交抛物线于点A,B,点A在点B的左侧,且两点均在第一象限,BH⊥CD于点H.设点A的横坐标为m.
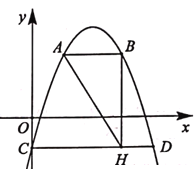
(1)当m=1时,求AB的长.
(2)若AH=![]() (CH-DH),求m的值.
(CH-DH),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,![]() 请根据上述条件,写出一个正确结论
请根据上述条件,写出一个正确结论![]() ”其中四位同学写出的结论如下:
”其中四位同学写出的结论如下:
小青:![]() ;小何:四边形DFBE是正方形;
;小何:四边形DFBE是正方形;
小夏:![]() ;小雨:
;小雨:![]() .
.
这四位同学写出的结论中不正确的是![]()
![]()

A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴、y轴分别交于A、B两点,点P从点A出发,沿折线AB﹣BO向终点O运动,在AB上以每秒5个单位长度的速度运动,在BO上以每秒3个单位长度的速度运动;点Q从点O出发,沿OA方向以每秒
与x轴、y轴分别交于A、B两点,点P从点A出发,沿折线AB﹣BO向终点O运动,在AB上以每秒5个单位长度的速度运动,在BO上以每秒3个单位长度的速度运动;点Q从点O出发,沿OA方向以每秒![]() 个单位长度的速度运动.P,Q两点同时出发,当点P停止时,点Q也随之停止.过点P作PE⊥AO于点E,以PE,EQ为邻边作矩形PEQF,设矩形PEQF与△ABO重叠部分图形的面积为S,点P运动的时间为t秒.
个单位长度的速度运动.P,Q两点同时出发,当点P停止时,点Q也随之停止.过点P作PE⊥AO于点E,以PE,EQ为邻边作矩形PEQF,设矩形PEQF与△ABO重叠部分图形的面积为S,点P运动的时间为t秒.
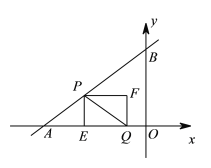
(1)连结PQ,当PQ与△ABO的一边平行时,求t的值;
(2)求S与t之间的函数关系式,并直接写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】熊组长准备为我们年级投资1万元围一个矩形的运动场地(如图),其中一边靠墙,另外三边选用不同材料建造且三边的总长为![]() ,墙长
,墙长![]() ,平行于墙的边的费用为200元/
,平行于墙的边的费用为200元/![]() ,垂直于墙的边的费用150元/
,垂直于墙的边的费用150元/![]() ,设平行与墙的边长为
,设平行与墙的边长为![]() .
.
(1)若运动场地面积为![]() ,求
,求![]() 的值;
的值;
(2)当运动场地的面积最大时是否会超了预算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,AD=BD,将△ABD绕点A逆时针旋转得到△ACE,使点C落在直线BD上.
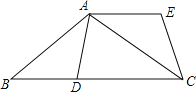
(1)求证:AE∥BC;
(2)连接DE,判断四边形ABDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产的一种果汁饮料由A、B两种水果配制而成,其比例与成本如下方表格所示,已知该饮料的成本价为8元/千克,按现价售出后可获利润50%,每个月可出售27500瓶.
每千克饮料所占比例 | 成本(元/千克) | |
A | 20% | m |
B | 80% | m-15 |
(1)求m的值;
(2)由于物价上涨,A水果成本提高了25%,B水果成本提高了20%,在不改变售价的情况下,若要保持每个月的利润不减少,则现在至少需要售出多少瓶饮料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为_____.
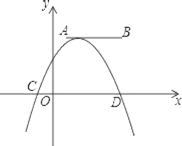
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且对称轴为直线
点,且对称轴为直线![]() ,点
,点![]() 坐标为
坐标为![]() .则下面的四个结论:①
.则下面的四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 或
或![]() .其中正确的是( )
.其中正确的是( )

A.①②B.①③C.①④D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com