
| 甲种机器 | 乙种机器 | |
| 价格/(万元/台) | 5 | 7 |
| 每台机器的日生产量/个 | 60 | 100 |
分析 (1)设购买甲种机器x台(x≥0),则购买乙种机器(6-x)台,根据买机器所耗资金不能超过34万元,即购买甲种机器的钱数+购买乙种机器的钱数≤34万元.就可以得到关于x的不等式,就可以求出x的范围.
(2)该公司购进的6台机器的日生产能力不能低于380个,就是已知不等关系:甲种机器生产的零件数+乙种机器生产的零件数≥380件.根据(1)中的三种方案,可以计算出每种方案的需要资金,从而选择出合适的方案.
解答 解:(1)设购买甲种机器x台,则购买乙种机器6-x台,
依题意得 5x+7(6-x)≤34,
解得x≥4,
∵6-x≥0,
∴x≤6,
∴x取4或5或6,
从而该公司有三种购买方案:①甲种机器4台,乙种机器2台;②甲种机器5台,乙种机器1台;③甲种机器6台;
(2)依题意得:60x+100(6-x)≥380,
解得$x≤5\frac{1}{2}$,由(1)知∴$4≤x≤5\frac{1}{2}$从而x取4或5,
当x=4时,购买资金为5×4+7×2=34(万元)
当x=5时,购买资金为5×5+7×1=32(万元)
所以应选择的购买方案是甲种机器5台,乙种机器1台.
点评 本题考查了一元一次不等式的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式,正确确定各种情况,确定各种方案是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
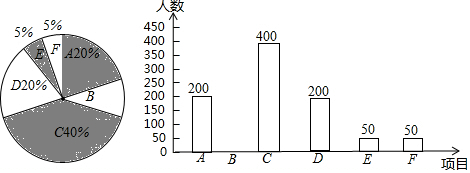
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
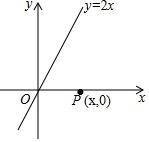 如图,已知直线y=2x和x轴上一动点P(x,0).
如图,已知直线y=2x和x轴上一动点P(x,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com