练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图①所示，在边长为1的正方形网格中放置了一个正方形ABCD．
    （1）应用割补法计算正方形ABCD的面积，并写出边长AB的长度；
    （2）在图②中，请画出面积为13的正方形EFGH，并写出线段EF的长度．
    精英家教网
    分析：（1）要求用割补法，即把图中面积相等且突出在外面的切掉补到空缺处，由图可把以AD为斜边的直角三角形切掉补到以BC为斜边的空白区，同样把以AB为斜边的直角三角形切掉补在以DC为斜边的空白区域，补好后可知总共为10个完整的正方形，即可得面积，再由面积即得AB的边长．
    （2）根据（1）题意可确定出面积为13的正方形EFGH，由面积即可得边长．
    解答：解：（1）由割补法可知，正方形ABCD可转化为10个小正方形，
    又每个小正方形的面积为1，所以正方形的面积为10，
    即AB2=10，
    ∴AB=
    		10
    ；

    （2）由（1）中图可知，面积为13的正方形EFGH边长为
    		13
    ，
    ∴每个斜边共占三列、两行方格，图形如下：
    精英家教网
    EF=
    		13
    ；
    点评：本题两小题都考查了正方形性质，而做第二题时要根据第一题总结规律．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    画图与计算：
    （1）如图1，正方形网格中的每个小正方形边长都是1，任意连接这些小正方形的顶点，可得到一些线段；请画出AB=
    		2
    ，CD=
    		5
    ，EF=
    		13
    这样的线段．
    （2）如图2所示，在边长为1 的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′，并计算对应点B和B′之间的距离．

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：013

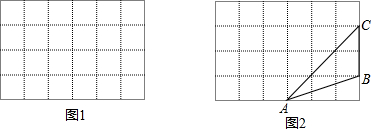
    如图1所示，在边长为a的正方形中挖去一个边长为b的小正方形(a＞b)，把余下的部分剪拼成一个矩形如图2，通过计算两个图形(阴影部分)的面积，验证了一个等式，则这个等式是

    [　　]

    A．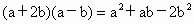

    B．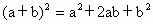

    C．

    D．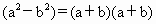

    查看答案和解析>>

    科目：初中数学 来源：学习周报　数学　华师大八年级版　2009－2010学年　第5期　总第161期 华师大版 题型：022

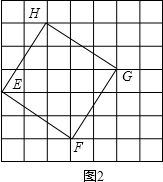
    如图1所示，在边长为a的正方形中剪去一个边长为b的小正方形(a＞b)，把剩下的部分延着虚线剪开，并且拼成一个梯形，如图2所示．分别计算这两个图形阴影部分的面积，验证了一个公式________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    画图与计算：
    （1）如图1，正方形网格中的每个小正方形边长都是1，任意连接这些小正方形的顶点，可得到一些线段；请画出AB=数学公式，CD=数学公式，EF=数学公式这样的线段．
    （2）如图2所示，在边长为1 的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′，并计算对应点B和B′之间的距离．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    画图与计算：
    （1）如图1，正方形网格中的每个小正方形边长都是1，任意连接这些小正方形的顶点，可得到一些线段；请画出AB=
    		2
    ，CD=
    		5
    ，EF=
    		13
    这样的线段．
    （2）如图2所示，在边长为1 的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′，并计算对应点B和B′之间的距离．

    精英家教网

    查看答案和解析>>

    同步练习册答案