练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知下列方程：①；②0.3x＝1；③；④x2﹣4x＝3；⑤x＝6；⑥x+2y＝0．其中一元一次方程的个数是（　　）

    A. 2B. 3C. 4D. 5

    【答案】B

    【解析】

    只含有一个未知数（元），并且未知数的指数是1（次）的方程叫做一元一次方程．

    解：①x2＝是分式方程，故①错误；
    ②0.3x=1，即0.3x-1=0，符合一元一次方程的定义．故②正确；
    ③＝5x+1，即9x+2=0，符合一元一次方程的定义．故③正确；
    ④x2-4x=3的未知数的最高次数是2，它属于一元二次方程．故④错误；
    ⑤x=6，即x-6=0，符合一元一次方程的定义．故⑤正确；
    ⑥x+2y=0中含有2个未知数，属于二元一次方程．故⑥错误．
    综上所述，一元一次方程的个数是3个．
    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我市新城区环形路的拓宽改造工程项目，经投标决定由甲、乙两个工程队共同完成这一工程项目．已知乙队单独完成这项工程所需天数是甲队单独完成这项工程所需天数的2倍；该工程如果由甲队先做6天，剩下的工程再由甲、乙两队合作16天可以完成．求甲、乙两队单独完成这项工程各需要多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，经过原点的抛物线y=﹣x2+2mx（m＞0）与x轴的另一个交点为A．过点P（1，m）作直线PM⊥x轴于点M，交抛物线于点B．记点B关于抛物线对称轴的对称点为C（B、C不重合）．连接CB，CP．

    （1）当m=3时，求点A的坐标及BC的长；
    （2）当m＞1时，连接CA，问m为何值时CA⊥CP？
    （3）过点P作PE⊥PC且PE=PC，问是否存在m，使得点E落在坐标轴上？若存在，求出所有满足要求的m的值，并定出相对应的点E坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解某品牌轿车的耗油情况，将油箱加满后进行了耗油试验，得到如表数据：

    轿车行驶的路程s(km)

    0

    100

    200

    300

    400

    …

    油箱剩余油量Q(L)

    50

    42

    34

    26

    18

    …

    (1)该轿车油箱的容量为______L，行驶150km时，油箱剩余油量为______L；

    (2)根据上表的数据，写出油箱剩余油量Q(L)与轿车行驶的路程s(km)之间的表达式；

    (3)某人将油箱加满后，驾驶该轿车从A地前往B地，到达B地时邮箱剩余油量为26L，求A，B两地之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下列证明过程．

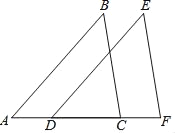
    如图，已知AB∥DE，AB＝DE，D，C在AF上，且AD＝CF，求证：△ABC≌△DEF．

    证明：∵AB∥DE

    ∴∠_____＝∠_____（_______）

    ∵AD＝CF

    ∴AD+DC＝CF+DC即_____

    在△ABC和△DEF中AB＝DE_____

    ∴△ABC≌△DEF_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

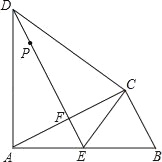
    【题目】如图，△ABC中，∠ACB＝90°，以AC为边在△ABC外作等边三角形ACD，过点D作AC的垂线，垂足为F，与AB相交于点E，连接CE．

    （1）说明：AE＝CE＝BE；

    （2）若AB＝15cm，P是直线DE上的一点．则当P在何处时，PB+PC最小，并求出此时PB+PC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，D是BC边上的中点，∠BDE=∠CDF，请你添加一个条件，使DE=DF成立．你添加的条件是 ．(不再添加辅助线和字母)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ABC=90°，CD⊥BC，BD与AC相交于点E，AB=9，BC=4，DC=3．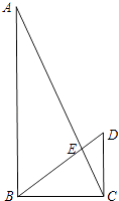

    （1）求BE的长度；
    （2）求△ABE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图甲，点C将线段AB分成两部分（AC＞BC），如果 = ，那么称点C为线段AB的黄金分割点．某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积分别为S1 ， S2（S1＞S2）的两部分，如果 = ，那么称直线l为该图形的黄金分割线．

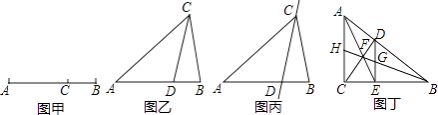
    （1）如图乙，在△ABC中，∠A=36°，AB=AC，∠ACB的平分线交AB于点D，请问点D是否是AB边上的黄金分割点，并证明你的结论；
    （2）若△ABC在（1）的条件下，如图丙，请问直线CD是不是△ABC的黄金分割线，并证明你的结论；
    （3）如图丁，在Rt△ABC中，∠ACB=90°，D为斜边AB上的一点，（不与A，B重合）过D作DE⊥BC于点E，连接AE，CD相交于点F，连接BF并延长，与DE，AC分别交于点G，H．请问直线BH是直角三角形ABC的黄金分割线吗？并说明理由．

    查看答案和解析>>

    同步练习册答案