
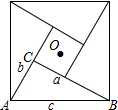
 在Rt△ABC中,∠ACB=90°,BC=a,AC=b.AB=c,将Rt△ABC绕点O依次旋转90°、180°和270°,构成的图形如图所示,该图是我国古代数学家赵爽制作的“勾股圆方图”,也被称作“赵爽弦图”,它是我国最早对勾股定理证明的记载,也成为了2002年在北京召开的国际数学家大会的会标设计的主要依据.
在Rt△ABC中,∠ACB=90°,BC=a,AC=b.AB=c,将Rt△ABC绕点O依次旋转90°、180°和270°,构成的图形如图所示,该图是我国古代数学家赵爽制作的“勾股圆方图”,也被称作“赵爽弦图”,它是我国最早对勾股定理证明的记载,也成为了2002年在北京召开的国际数学家大会的会标设计的主要依据.分析 (1)根据题意,我们可在图中找等量关系,由中间的小正方形的面积等于大正方形的面积减去四个直角三角形的面积,列出等式化简即可得出勾股定理的表达式.
(2)利用非负数的性质证明即可.
(3)把a、b的值代入a2+b2≥2ab中,进行计算得到a+b≥2$\sqrt{ab}$.利用该结论求得当x,y取何值时,该矩形面积最大以及其最大面积.
解答 解:(1)∵大正方形面积为c2,直角三角形面积为$\frac{1}{2}$ab,小正方形面积为:(b-a)2,
∴c2=4×$\frac{1}{2}$ab+(a-b)2=2ab+a2-2ab+b2
即c2=a2+b2.
(2)∵(a-b)2≥0,
∴a2-2ab+b2≥0,
∴a2+b2≥2ab,
当且仅当a=b时,等号成立.
(3)把a=$\sqrt{x}$,b=$\sqrt{y}$,代入a2+b2≥2ab中得到:a+b≥2$\sqrt{ab}$.
依题意得:x+y=8.
则x+y≥2$\sqrt{xy}$,即8≥2$\sqrt{xy}$,
∴xy≤16,
当且仅当x=y=4时取“=”.
∴当x=y=4时,该矩形面积最大,最大面积是16.
点评 本题考查了四边形综合题.需要学生掌握勾股定理的证明和以及非负数的性质,掌握三角形和正方形面积计算公式是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 如图,点C是反比例函数y=$\frac{k}{x}$图象的一点,点C的坐标为(4,-1).
如图,点C是反比例函数y=$\frac{k}{x}$图象的一点,点C的坐标为(4,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
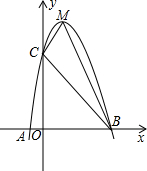 已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com