
如图,平面直角坐标系中,直线AB与![]() 轴,
轴,![]() 轴分别交于A(3,0),B(0,
轴分别交于A(3,0),B(0,![]() )两点, ,点C为线段AB上的一动点,过点C作CD⊥
)两点, ,点C为线段AB上的一动点,过点C作CD⊥![]() 轴于点D.
轴于点D.
(1)求直线AB的解析式;
(2)若S梯形OBCD=![]() ,求点C的坐标;
,求点C的坐标;
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的
三角形与△OBA相似.若存在,请求出所有符合条件
的点P的坐标;若不存在,请说明理由.(做出一种答案即可)

(1)直线AB解析式为:y=![]() x+
x+![]() .
.
(2)方法一:设点C坐标为(x,![]() x+
x+![]() ),那么OD=x,CD=
),那么OD=x,CD=![]() x+
x+![]() .
.
∴![]() =
=![]() =
=![]() .
.
由题意:![]() =
=![]() ,解得
,解得![]() (舍去)
(舍去)
∴ C(2,![]() )
)
方法二:∵ ![]() ,
,![]() =
=![]() ,∴
,∴![]() .
.
由OA=![]() OB,得∠BAO=30°,AD=
OB,得∠BAO=30°,AD=![]() CD.
CD.
∴ ![]() =
=![]() CD×AD=
CD×AD=![]() =
=![]() .可得CD=
.可得CD=![]() .
.
 ∴ AD=1,OD=2.∴C(2,
∴ AD=1,OD=2.∴C(2,![]() ).
).
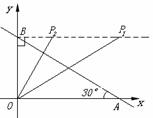
(3)当∠OBP=Rt∠时,如图
①若△BOP∽△OBA,则∠BOP=∠BAO=30°,BP=![]() OB=3,
OB=3,
∴![]() (3,
(3,![]() ).
).
②若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=![]() OB=1.
OB=1.
∴![]() (1,
(1,![]() ).
).
当∠OPB=Rt∠时
③ 过点P作OP⊥BC于点P(如图),此时△PBO∽△OBA,∠BOP=∠BAO=30°
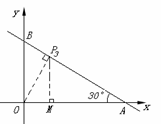 过点P作PM⊥OA于点M.
过点P作PM⊥OA于点M.
方法一: 在Rt△PBO中,BP=![]() OB=
OB=![]() ,OP=
,OP=![]() BP=
BP=![]() .
.
∵ 在Rt△PMO中,∠OPM=30°,
∴ OM=![]() OP=
OP=![]() ;PM=
;PM=![]() OM=
OM=![]() .∴
.∴![]() (
(![]() ,
,![]() ).
).
 方法二:设P(x ,
方法二:设P(x ,![]() x+
x+![]() ),得OM=x ,PM=
),得OM=x ,PM=![]() x+
x+![]()
由∠BOP=∠BAO,得∠POM=∠ABO.
∵tan∠POM==![]() =
=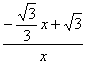 ,tan∠ABOC=
,tan∠ABOC=![]() =
=![]() .
.
∴![]() x+
x+![]() =
=![]() x,解得x=
x,解得x=![]() .此时,
.此时,![]() (
(![]() ,
,![]() ).
).
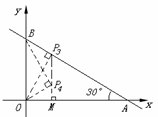
④若△POB∽△OBA(如图),则∠OBP=∠BAO=30°,∠POM=30°.
∴ PM=![]() OM=
OM=![]() .
.
∴ ![]() (
(![]() ,
,![]() )(由对称性也可得到点
)(由对称性也可得到点![]() 的坐标).
的坐标).
当∠OPB=Rt∠时,点P在x轴上,不符合要求.
综合得,符合条件的点有四个,分别是:
![]() (3,
(3,![]() ),
),![]() (1,
(1,![]() ),
),![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
 11、象棋中的马走日字对角(如图1由点A到点B或由点A到点C),现建立如图2平面直角坐标系,则下一步可能到达的点的坐标是
11、象棋中的马走日字对角(如图1由点A到点B或由点A到点C),现建立如图2平面直角坐标系,则下一步可能到达的点的坐标是查看答案和解析>>
科目:初中数学 来源: 题型:
| k | x |
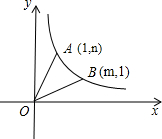 OA、OB.
OA、OB.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图平面直角坐标系中,已知点A的坐标为(-3,-1),点B的坐标为(2,-4).
如图平面直角坐标系中,已知点A的坐标为(-3,-1),点B的坐标为(2,-4).查看答案和解析>>
科目:初中数学 来源: 题型:
 在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),
在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com