
【题目】已知关于x的方程x2﹣(k+1)x+![]() k2+1=0有两个实数根.
k2+1=0有两个实数根.
(1)求k的取值范围;
(2)若抛物线y=x2﹣(k+1)x+![]() k2+1与x轴交于A、B两点,点A、点B到原点O的距离分别为OA、OB,且满足OA+OB﹣4OAOB+5=0,求k的值.
k2+1与x轴交于A、B两点,点A、点B到原点O的距离分别为OA、OB,且满足OA+OB﹣4OAOB+5=0,求k的值.
【答案】(1)、k≥![]() ;(2)、k=2.
;(2)、k=2.
【解析】
试题分析:(1)、由于关于x的一元二次方程x2﹣(2k+1)x+k2+2k=0有两个实数根,可知△≥0,据此进行计算即可; (2)、由根与系数的关系和已知条件得出关于k的方程,解方程即可.
试题解析:(1)、∵原方程有两个实数根, ∴△=(k+1)2﹣4(![]() k2+1)≥0 ∴k2+2k+1﹣k2﹣4≥0,
k2+1)≥0 ∴k2+2k+1﹣k2﹣4≥0,
解得:k≥![]()
(2)、设A、B两点的坐标为A(x1,0)、B(x2,0) 则x1、x2是方程x2﹣(k+1)x+![]() k2+1=0的两根
k2+1=0的两根
∵k≥![]() , ∴x1+x2=k+1>0,x1x2=
, ∴x1+x2=k+1>0,x1x2=![]() k2+1>0, ∴x1>0,x2>0, ∴OA+OB=|x1|+|x2|=x1+x2=k+1 OAOB=|x1||x2|=4x1x2﹣5 ∴k+1=4(
k2+1>0, ∴x1>0,x2>0, ∴OA+OB=|x1|+|x2|=x1+x2=k+1 OAOB=|x1||x2|=4x1x2﹣5 ∴k+1=4(![]() k2+1)﹣5, ∴k2﹣k+2=0, ∴k1=﹣1,k2=2,
k2+1)﹣5, ∴k2﹣k+2=0, ∴k1=﹣1,k2=2,
又∵k≥![]() , ∴k=2
, ∴k=2


科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小;
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?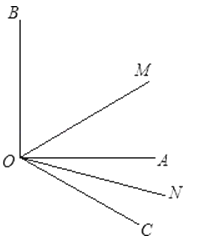
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.同旁内角互补
B.一组数据的方差越大,这组数据波动性越大
C.若∠α=72°55′,则∠α的补角为107°45'
D.对角线互相垂直的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD(四边相等,四个角都是直角)的边长为4,点P从点A出发,以每秒1个单位长度的速度沿射线AD向点D运动;点Q从点D同时出发,以相同的速度沿射线AD方向向右运动,当点P到达点D时,点Q也停止运动,连接BP,过点P作BP的垂线交过点Q平行于CD的直线l于点E,BE于CD相交于点F,连接PF,设点P运动时间为t(s),
(1)求∠PBE的度数;
(2)当t为何值时,△PQF是以PF为腰的等腰三角形?
(3)试探索在运动过程中△PDF的周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
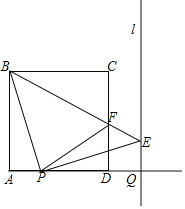
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,|4-(-2)|表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离;同理|x-3|也可理解为x与3两数在数轴上所对应的两点之间的距离,试探索并完成填空.
(1)求|4-(-2)|=______,|-3-5|=______;
(2)若|x-2|=5,则x=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com