
分析 (1)可以把二次根式化简,合并括号里同类二次根式,再做除法;
(2)化简,合并同类二次根式;
(3)用分配律计算,然后化简,合并同类二次根式;
(4)化简,合并同类二次根式即可.
解答 解:(1)(3$\sqrt{15}$+$\sqrt{\frac{3}{5}}$)÷$\sqrt{5}$
=(3$\sqrt{15}$+$\frac{\sqrt{15}}{5}$)÷$\sqrt{5}$
=$\frac{16\sqrt{15}}{5}$÷$\sqrt{5}$
=$\frac{16\sqrt{3}}{5}$;
(2)$\sqrt{12}$-$\sqrt{\frac{1}{3}}$-$\sqrt{1\frac{1}{3}}$
=2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$-$\frac{2\sqrt{3}}{3}$
=$\sqrt{3}$;
(3)$\sqrt{2}$(1+2$\sqrt{3}$)+(-2)2-(1-$\sqrt{3}$)0-$\sqrt{24}$
=$\sqrt{2}$+2$\sqrt{6}$+4-1-2$\sqrt{6}$
=$\sqrt{2}$+3;
(4)$\sqrt{18}$-$\frac{2}{{\sqrt{2}}}$-$\frac{{\sqrt{8}}}{2}$+($\sqrt{5}$-1)0
=3$\sqrt{2}$-$\sqrt{2}$-$\sqrt{2}$+1
=$\sqrt{2}$+1.
点评 本题考查了二次根式的混合运算,在二次根式的混合运算中,要掌握好运算顺序及各运算律.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:填空题
 已知在Rt△ABC中,BC=6,CD是斜边AB上的中线,点G是△ABC的重心,将△ADC绕重点G旋转,得到△A1D1C1,并且C1D1∥AB,直线A1D1⊥AC,设直线A1C1、A1D1分别交AC于点E,F,那么EF的长为$\frac{5\sqrt{3}}{3}$或3$\sqrt{3}$.
已知在Rt△ABC中,BC=6,CD是斜边AB上的中线,点G是△ABC的重心,将△ADC绕重点G旋转,得到△A1D1C1,并且C1D1∥AB,直线A1D1⊥AC,设直线A1C1、A1D1分别交AC于点E,F,那么EF的长为$\frac{5\sqrt{3}}{3}$或3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
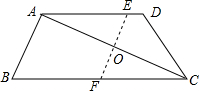 如图,在四边形ABCD中,AD∥BC,把四边形对折,使点A、C重合,折痕EF分别交AD于点E,交BC于点F.
如图,在四边形ABCD中,AD∥BC,把四边形对折,使点A、C重合,折痕EF分别交AD于点E,交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,AD=9,如果$\frac{BE}{BC}$=$\frac{2}{3}$,那么$\frac{BF}{FD}$=$\frac{2}{3}$,BE=6.
如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,AD=9,如果$\frac{BE}{BC}$=$\frac{2}{3}$,那么$\frac{BF}{FD}$=$\frac{2}{3}$,BE=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图△ABC中,D、E、F分别是AB、AC、BC的中点.
已知:如图△ABC中,D、E、F分别是AB、AC、BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com