
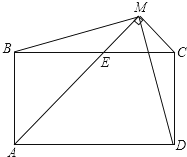
 如图,已知矩形ABCD中,过点C引∠A的平分线AM的垂线,垂足为M,AM交BC于E,连接MB,MD.
如图,已知矩形ABCD中,过点C引∠A的平分线AM的垂线,垂足为M,AM交BC于E,连接MB,MD.分析 (1)由矩形的性质得出AB=DC,AD=BC,∠BAD=∠ABC=90°,证出∠BAE=∠AEB,得出BE=AB,即可得出结论;
(2)先证△MEC是等腰直角三角形,得出ME=MC,∠MCE=45°,再证出∠BEM=∠DCM,由SAS证明△MBE≌△MDC,得出对应角相等即可;
(3)作BG⊥AM于G,作DH⊥AM于H,由三角函数求出BG、DH,再求出AM,四边形ABMD面积=△ABM的面积+△ADM的面积,即可得出结果.
解答 (1)证明:∵四边形ABCD是矩形,
∴AB=DC,AD=BC,∠BAD=∠ABC=90°,
∵AM平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=DC;
(2)证明:∵∠AEB=45°,
∴∠BEM=135°,∠MEC=45°,
∵CM⊥AM,
∴△MEC是等腰直角三角形,
∴ME=MC,∠MCE=45°,
∴∠DCM=135°,
∴∠BEM=∠DCM,
在△MBE和△MDC中,$\left\{\begin{array}{l}{BE=DC}&{\;}\\{∠BEM=∠DCM}&{\;}\\{ME=MC}&{\;}\end{array}\right.$,
∴△MBE≌△MDC(SAS),
∴∠MBE=∠MDC;
(3)解:作BG⊥AM于G,作DH⊥AM于H,如图所示: 则∠AGB=∠AHD=90°,
则∠AGB=∠AHD=90°,
∴BG=$\frac{\sqrt{2}}{2}$AB=3$\sqrt{2}$,DH=$\frac{\sqrt{2}}{2}$AD=5$\sqrt{2}$,
∵BE=AB=6,
∴AE=$\sqrt{2}$AB=6$\sqrt{2}$,CE=4,
∴ME=$\frac{\sqrt{2}}{2}$CE=2$\sqrt{2}$,
∴AM=AE+ME=8$\sqrt{2}$,
∴四边形ABMD面积=△ABM的面积+△ADM的面积
=$\frac{1}{2}$AM•BG+$\frac{1}{2}$AM•DH=$\frac{1}{2}$AM(BG+DH)
=$\frac{1}{2}$×8$\sqrt{2}$×8$\sqrt{2}$
=64;
故答案为:64.
点评 本题考查了矩形的性质、等腰三角形的判定、等腰直角三角形的判定与性质、全等三角形的判定与性质、三角函数、三角形面积的计算;熟练掌握矩形的性质,并能进行推理论证与计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com