
已知抛物线y=-x2+2mxm2m+2.
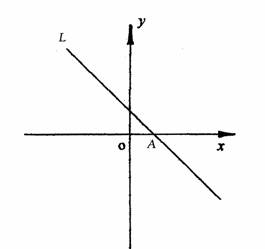
(1)判断抛物线的顶点与直线L:y=-x+2的位置关系;
(2)设该抛物线与x轴交于M、N两点,当OM?ON=4,且OM≠ON时,求出这条抛物线的解析式;
(3)直线L交x轴于点A,(2)中所求抛物线的对称轴与x轴交于点B.那么在对称轴上是否存在点P,使⊙P与直线L和x轴同时相切.若存在,求出点P的坐标;若不存在,请说明理由.
(1)由抛物线![]() ,得顶点坐标为
,得顶点坐标为
(m,-m+2), 显然满足y=-x+2
∴ 抛物线的顶点在直线L上.
(2)设M(![]() ,0),N(
,0),N(![]() ,0),且
,0),且![]() . 由OM?ON=4,,OM≠ON,得
. 由OM?ON=4,,OM≠ON,得![]() .
.
∵ ![]() , ∴
, ∴ ![]() .
.
当![]() 时,
时, ![]() ,
,![]()
当![]() 时,<0,此方程无解
时,<0,此方程无解
∵ △1=(2m)![]() -4(m
-4(m![]() +m-2)=-4m+8=-4m+8>0. ∴ m<2.
+m-2)=-4m+8=-4m+8>0. ∴ m<2.
故取m=-3.
则抛物线的解析式为![]() .
.
(3)抛物线![]() 的对称轴为x=-3,顶点(-3,5).
的对称轴为x=-3,顶点(-3,5).
依题意,∠CAB=∠ACB=45°.
若点P在x轴的上方,设![]() (-3,a)(a>0),则点
(-3,a)(a>0),则点![]() 到直线L的距离
到直线L的距离![]() 为a(如图), ∴ △
为a(如图), ∴ △![]() 是等腰直角三角形.
是等腰直角三角形.
∴ ![]() ,
,![]() . ∴
. ∴ ![]() ,5
,5![]() .
.
 若点P在x轴的下方,设
若点P在x轴的下方,设![]() (-3,-b)(b>0), 则点
(-3,-b)(b>0), 则点![]() 到直线L的距离
到直线L的距离![]() 为b(如图),同理可得△
为b(如图),同理可得△![]() 为等腰直角三角形,
为等腰直角三角形,
∴ ![]() ,
,![]() . ∴
. ∴ ![]() ,
,![]() .
.
∴ 满足条件的点有两个,即(-3,![]() )和(-3,
)和(-3,![]() ).
).


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
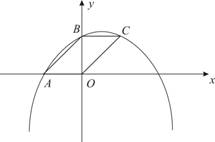
如图,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB.
1.求b+c的值
2.若点C在抛物线上,且四边形OABC是平行四边形,试求抛物线的解析式;
3.在(2)的条件下,作∠OBC的角平分线,与抛物线交于点P,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2011届广东省深圳市华富中学初三上学期期中数学卷 题型:解答题
已知抛物线y=-x2+mx-m+2.
(Ⅰ)若抛物线与x轴的两个交点A、B分别在原点的两侧,并且AB=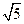 ,试求m的值;
,试求m的值;
(Ⅱ)设C为抛物线与y轴的交点,若抛物线上存在关于原点对称的两点M、N,并且 △MNC的面积等于27,试求m的值
查看答案和解析>>
科目:初中数学 来源:2010-2011学年度潍坊市高密七年级第二学期期末考试数学 题型:解答题
(11·兵团维吾尔)(8分)已知抛物线y=-x2+4x-3与x轴交于A、B两点(A
点在B点左侧),顶点为P.
(1)求A、B、P三点的坐标;
(2)在 直角坐标系中,用列表描点法作出抛物线的图象,并根据图象写出x取何值时,函
直角坐标系中,用列表描点法作出抛物线的图象,并根据图象写出x取何值时,函
数值大于零;
(3)将此抛物线的图象向下平移一个单位,请写出平称后图象的函数表达式.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建尤溪初中毕业学业质量检测数学试卷(解析版) 题型:解答题
如图,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB.
1.求b+c的值
2.若点C在抛物线上,且四边形OABC是平行四边形,试求抛物线的解析式;
3.在(2)的条件下,作∠OBC的角平分线,与抛物线交于点P,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源:2011-2012学年苏州市区九年级上学期期末考试数学卷 题型:填空题
(本题满分5分)已知抛物线y=-x2+bx+c,它与x轴的两个交点分别为(-1,0),(3,0),求此抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com