
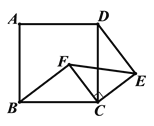
【题目】如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF, BC=5,CF=3,BF=4.
求证:DE∥FC
【答案】证明见解析.
【解析】试题分析:根据正方形以及△ECF的性质得出△BCF和△DCE全等,从而得出∠DEC=∠BFC,根据BC、CF和BF的长度得出∠BFC=90°,即∠DEC=90°,最后根据同旁内角互补两直线平行得出答案.
试题解析:∵四边形 ABCD是正方形 ∴∠BCF+∠FCD=90°,BC=CD,
∵△ECF是等腰直角三角形, ∴∠ECD+∠FCD=90°, CF=CE,
∴∠BCF=∠ECD, ∴△BCF≌△DCE,
在△BFC中,BC=5,CF=3,BF=4, ∴ CF2+BF2=BC2 ∴∠BFC=90°,
∵△BCF≌△DCE,∴DE=BF=4,∠BFC=∠DEC=∠FCE=90°,∴DE∥FC.


科目:初中数学 来源: 题型:
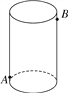
【题目】如图,圆柱形玻璃容器高19cm,底面周长为60cm,在外侧距下底1.5cm的点A处有一只蜘蛛,在蜘蛛正对面的圆柱形容器的外侧,距上底1.5cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与直线l交于点A、B两点,且A点为抛物线与y轴的交点,B(﹣2,﹣4),抛物线的对称轴是直线x=2,过点A作AC⊥AB,交抛物线于点C、x轴于点D.
(1)求此抛物线的解析式;
(2)求点D的坐标;
(3)抛物线上是否存在点K,使得以AC为边的平行四边形ACKL的面积等于△ABC的面积?若存在,请直接写出点K的横坐标;若不存在,请说明理由.[提示:抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣ ![]() ,顶点坐标为(﹣
,顶点坐标为(﹣ ![]() ,
, ![]() )].
)].
查看答案和解析>>
科目:初中数学 来源: 题型:
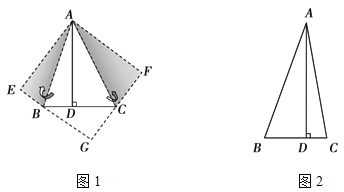
【题目】如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长. 小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,即可求出x的值.参考小萍的思路,探究并解答新问题:如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有3个相同的小球,它们分别写有数值﹣1,1,5;乙口袋中装有3个相同的小球,它们分别写有数值﹣4,2,3.现从甲口袋中随机取一球,记它上面的数值为x,再从乙口袋中随机取一球,记它上面的数值为y.设点A的坐标为(x,y),请用树形图或列表法,求点A落在第一象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的球形容器上连接着两根导管,容器中盛满了不溶于水的比空气重的某种气体,现在要用向容器中注水的方法来排净里面的气体.水从左导管匀速地注入,气体从右导管排出,那么,容器内剩余气体的体积与注水时间的函数关系的大致图象是( ) 
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com