
 如图所示,AB是⊙O的直径,CD是⊙O的一条弦,延长DC与BA的延长线相交于点P,且PC=OB,∠BOD=99°,求∠P的度数.
如图所示,AB是⊙O的直径,CD是⊙O的一条弦,延长DC与BA的延长线相交于点P,且PC=OB,∠BOD=99°,求∠P的度数. 科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于点D,
如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于点D,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a+2b=5 | B. | a5÷a=a4 | C. | (-2a2)3=-6a6 | D. | 3a-2=$\frac{1}{9{a}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
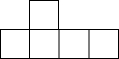 张明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.
张明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为ts.
已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
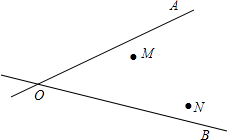 某地有两个村庄M、N和两条相交叉的公路OA,OB,现计划修建一个物资仓库,希望仓库到两个村庄的距离相等,到两条公路的距离也相等,请你用尺规作图的方法确定该点P.(注意保留作图痕迹,不用写作法)
某地有两个村庄M、N和两条相交叉的公路OA,OB,现计划修建一个物资仓库,希望仓库到两个村庄的距离相等,到两条公路的距离也相等,请你用尺规作图的方法确定该点P.(注意保留作图痕迹,不用写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,根据三角函数定义尝试说明:
如图,在Rt△ABC中,∠C=90°,根据三角函数定义尝试说明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com