
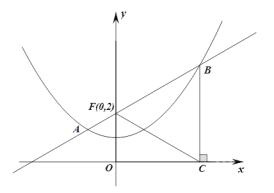
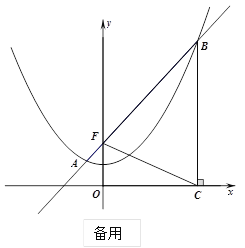
【题目】如图,已知抛物线![]() 过点
过点![]() ,过定点
,过定点![]() 的直线
的直线![]() :
:![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,过点
的右侧,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 在x轴上运动,连接
在x轴上运动,连接![]() ,作
,作![]() 的垂直平分线与过点D作x轴的垂线交于点
的垂直平分线与过点D作x轴的垂线交于点![]() ,判断点
,判断点![]() 是否在抛物线
是否在抛物线![]() 上,并证明你的判断;
上,并证明你的判断;
(3)若![]() ,设
,设![]() 的中点为
的中点为![]() ,抛物线上是否存在点
,抛物线上是否存在点![]() ,使得
,使得![]() 周长最小,若存在求出周长的最小值,若不存在说明理由;
周长最小,若存在求出周长的最小值,若不存在说明理由;
(4)若![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使得
,使得![]() 的面积为
的面积为![]() ,若存在求出点
,若存在求出点![]() 的坐标,若不存在说明理由.
的坐标,若不存在说明理由.
【答案】(1)![]() ;(2)在,理由详见解析;(3)存在,
;(2)在,理由详见解析;(3)存在,![]() ;(4)存在,
;(4)存在,![]() 或
或![]() 或
或![]()
【解析】
(1)抛物线![]() 过点
过点![]() ,利用待定系数法即可求解;
,利用待定系数法即可求解;
(2)设I的坐标为![]() ,过I作IH⊥y轴于点H,由点I在线段DF的垂直平分线上,求得ID=IF=y,在Rt
,过I作IH⊥y轴于点H,由点I在线段DF的垂直平分线上,求得ID=IF=y,在Rt![]() 中,利用勾股定理计算,求得得点I的坐标为
中,利用勾股定理计算,求得得点I的坐标为![]() ,从而说明点
,从而说明点![]() 在抛物线上;
在抛物线上;
(3)先求得![]() 的中点M的坐标为
的中点M的坐标为![]() ,作PN⊥
,作PN⊥![]() 轴于点N,利用(2)的结论:抛物线上的点到点F的距离等于它到
轴于点N,利用(2)的结论:抛物线上的点到点F的距离等于它到![]() 轴的距离,当
轴的距离,当![]() 三点共线时,
三点共线时,![]() 周长最小,即可求得答案;
周长最小,即可求得答案;
(4)作QR⊥![]() 轴于点D,交AB于点R,先求得直线
轴于点D,交AB于点R,先求得直线![]() 的解析式和点
的解析式和点![]() 的坐标,利用三角形面积公式求得
的坐标,利用三角形面积公式求得![]() ,再求得
,再求得![]() ,设点
,设点![]() 的坐标为:
的坐标为:![]() ,则点
,则点![]() 的坐标为:
的坐标为:![]() ,则
,则![]() ,解方程即可求得点
,解方程即可求得点![]() 的坐标.
的坐标.
(1)∵抛物线![]() 过点
过点![]() ,
,
∴ ,
,
解得:![]() ,
,
∴抛物线的解析式为:![]() ;
;
(2)在,理由如下:
设I的坐标为![]() ,过I作IH⊥y轴于点H,如图:
,过I作IH⊥y轴于点H,如图:
则![]() ,
,![]() ,
,
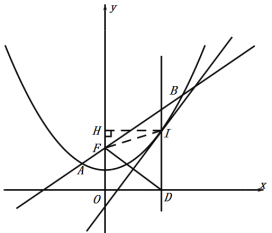
∵点I在线段DF的垂直平分线上,
∴ID=IF=y,
在Rt![]() 中,
中,![]() ,
,
∴![]() ,
,
化简得:![]() ,
,
∴点I![]() 在抛物线
在抛物线![]() 上;
上;
(3)存在,理由如下:
若![]() ,设
,设![]() 的中点为
的中点为![]() ,
,
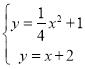 ,
,
消去y得:![]() ,
,
∴点M的横坐标为:![]() ,
,
纵坐标为:![]() ,
,
∴点M的坐标为:![]() ,
,
由(2)可知:抛物线上的点到点F的距离等于它到![]() 轴的距离,
轴的距离,
设抛物线上存在点P,使得![]() 周长最小,
周长最小,
过点P作PN⊥![]() 轴于点N,如图:
轴于点N,如图:
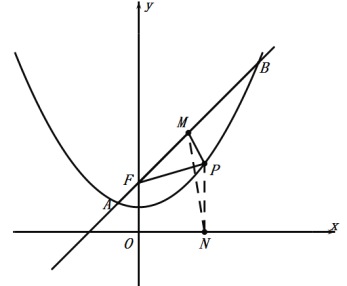
∵![]() ,
,
由于![]() 是定值,
是定值,![]() ,
,
∴当![]() 三点共线,即
三点共线,即![]() ⊥
⊥![]() 轴于点N时,
轴于点N时,![]() 周长最小,
周长最小,
此时点![]() 的坐标为:
的坐标为:![]() ,
,![]() ,
,
![]() ,
,
∴![]() 周长最小值为:
周长最小值为:![]() ;
;
(4)存在,理由如下:
过点Q作QR⊥![]() 轴于点D,交AB于点R,如图,
轴于点D,交AB于点R,如图,
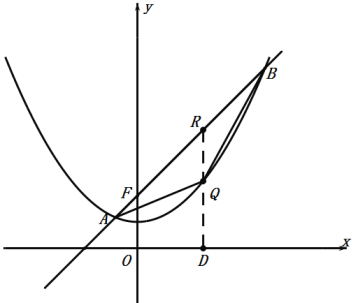
将![]() 代入
代入![]() 得:
得:![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
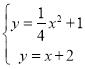
解得: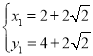 ,
,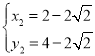 ,
,
∴点![]() 的坐标为:
的坐标为:![]() ,
,
![]() ,
,
∵![]() 的面积为
的面积为![]() ,
,
∴![]() ,
,
∴![]() ,
,
设点![]() 的坐标为:
的坐标为:![]() ,则点
,则点![]() 的坐标为:
的坐标为:![]() ,
,
∴![]() ,
,
当![]() 时,
时,
解得:![]() ,此时点
,此时点![]() 的坐标为:
的坐标为:![]() ,
,
当![]() 时,即
时,即![]() ,
,
![]() ,
,
解得:![]() 或
或![]() ,此时点
,此时点![]() 的坐标为:
的坐标为:![]() 或
或![]() ,
,
综上:满足条件的点![]() 为:
为:![]() 或
或![]() 或
或![]() .
.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D,E分别是边AB,AC上的点,DE∥BC,点H是边BC上的点,连接AH交线段DE于点G,且BH=DE=12,DG=8,S△ADG=12,则S四边形BCED=( )

A.24B.22.5C.20D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() ,
,![]() ,
,![]() .点
.点![]() 从
从![]() 开始沿边
开始沿边![]() 向点
向点![]() 以
以![]() 的速度移动,与此同时,点
的速度移动,与此同时,点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向点
向点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当点
同时出发,当点![]() 运动到点
运动到点![]() 时,两点停止运动,问:
时,两点停止运动,问:
![]() 经过几秒,
经过几秒,![]() 的面积等于
的面积等于![]() ?
?
(2)![]() 的面积会等于
的面积会等于![]() 吗?若会,请求出此时的运动时间;若不会,请说明理由.
吗?若会,请求出此时的运动时间;若不会,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
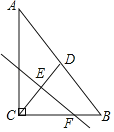
【题目】如图所示,在△ABC中,∠C=90°,AB=8,CD是AB边上的中线,作CD的中垂线与CD交于点E,与BC交于点F.若CF=x,tanA=y,则x与y之间满足( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,M、N分别是边AD、BC边上的中点,且△ABM≌△DCM;E、F分别是线段BM、CM的中点.
(1)求证:平行四边形ABCD是矩形.
(2)求证:EF与MN互相垂直.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方方驾驶小汽车匀速地从A地行使到B地,行驶里程为480千米,设小汽车的行使时间为t(单位:小时),行使速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
⑴求v关于t的函数表达式;
⑵方方上午8点驾驶小汽车从A出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() ,的图象和性质进行了探究过程如下,请补充完成:
,的图象和性质进行了探究过程如下,请补充完成:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________________;
的取值范围是__________________;
(2)下表是![]() 与
与![]() 的几组对应值.请直接写出
的几组对应值.请直接写出![]() ,
,![]() 的值:
的值:![]() ______________;
______________;![]() ________.
________.
| … |
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| -3 | 5 | 3 |
|
| … |
(3)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
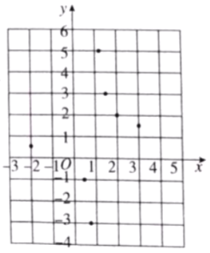
(4)通过观察函数的图象,小明发现该函数图象与反比例函数![]() 的图象形状相同,是中心对称图形,且点
的图象形状相同,是中心对称图形,且点![]() 和
和![]() 是一组对称点,则其对称中心的坐标为________.
是一组对称点,则其对称中心的坐标为________.
(5)请写出一条该函数的性质:___________________.
(6)当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有实数解,求
有实数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.(如图所示)一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=50米,若灰太狼以5米/秒的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com