
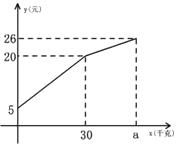
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,在 ![]() 中,
中, ![]() ,AC=BC,
,AC=BC, ![]() ,
, ![]() ,垂足分别为D,E.
,垂足分别为D,E.
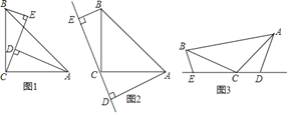
(1)若AD=2.5cm,DE=1.7cm,求BE的长.
(2)如图2,在原题其他条件不变的前提下,将CE所在直线旋转到 ![]() ABC的外部,请你猜想AD,DE,BE三者之间的数量关系,直接写出结论:________.(不需证明)
ABC的外部,请你猜想AD,DE,BE三者之间的数量关系,直接写出结论:________.(不需证明)
(3)如图3,若将原题中的条件改为:“在 ![]() ABC中,AC=BC,D,C,E三点在同一条直线上,并且有
ABC中,AC=BC,D,C,E三点在同一条直线上,并且有 ![]() ,其中
,其中 ![]() 为任意钝角”,那么(2)中你的猜想是否还成立?若成立,请予以证明;若不成立,请说明理由.
为任意钝角”,那么(2)中你的猜想是否还成立?若成立,请予以证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
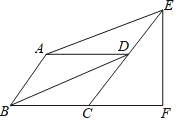
【题目】如图,平行四边形ABCD中,E,F分别在CD、BC的延长线上,AE∥BD,EF⊥BC,tan∠ABC=![]() ,EF=,则AB的长为( )
,EF=,则AB的长为( )
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
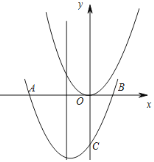
【题目】如图,在平面直角坐标系xOy中,将抛物线y=x2平移,使平移后的抛物线经过点A(–3,0)、B(1,0).
(1)求平移后的抛物线的表达式.
(2)设平移后的抛物线交y轴于点C,在平移后的抛物线的对称轴上有一动点P,当BP与CP之和最小时,P点坐标是多少?
(3)若y=x2与平移后的抛物线对称轴交于D点,那么,在平移后的抛物线的对称轴上,是否存在一点M,使得以M、O、D为顶点的三角形△BOD相似?若存在,求点M坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
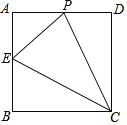
【题目】如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿![]() 移动至终点C.设点P经过的路径长为x,
移动至终点C.设点P经过的路径长为x,![]() 的面积为y,则下列图象能大致反映y与x之间的函数关系的是( )
的面积为y,则下列图象能大致反映y与x之间的函数关系的是( )
A.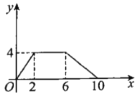 B.
B.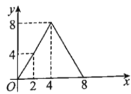
C.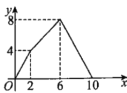 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A,B两城决定向C,D两乡运送肥料以支持农村生产.已知A,B两城分别有肥料210吨和290吨,从A城往C,D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C,D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)设从A城运往C乡肥料x吨.
①用含x的代数式完成下表:
C乡(吨) | D乡(吨) | |
A城 | x | |
B城 | ||
总计 | 240 | 260 |
②设总运费为y元,写出y与x的函数关系式,并求出最少总运费;
(2)由于更换车型,使从A城往C乡运肥料的费用每吨减少a(![]() )元,这时从A城往C乡运肥料多少吨时总运费最少?
)元,这时从A城往C乡运肥料多少吨时总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
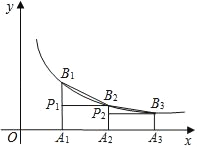
【题目】如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3=…=An﹣1An=1,分别过点A1、A2、A3、An作x轴的垂线,交反比例函数y=![]() (x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2018=_____.
(x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2018=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,随着电子产品的广泛应用,学生的近视发生率出现低龄化趋势,引起了相关部门的重视.某区为了了解在校学生的近视低龄化情况,对本区7-18岁在校近视学生进行了简单的随机抽样调查,并绘制了以下两幅不完整的统计图.

请根据图中信息,回答下列问题:
(1)这次抽样调查中共调查了近视学生 人;
(2)请补全条形统计图;
(3)扇形统计图中10-12岁部分的圆心角的度数是 ;
(4)据统计,该区7-18岁在校学生近视人数约为10万,请估计其中7-12岁的近视学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与x轴从左至右交于A,B两点,与y轴交于点c.
与x轴从左至右交于A,B两点,与y轴交于点c.

(1)若抛物线过点T(1,-![]() ),求抛物线的解析式;
),求抛物线的解析式;
(2)在第二象限内的抛物线上是否存在点D,使得以A、B、D三点为顶点的三角形与△ABC相似?若存在,求a的值;若不存在,请说明理由.
(3)如图2,在(1)的条件下,点P的坐标为(-1,1),点Q(6,t)是抛物线上的点,在x轴上,从左至右有M、N两点,且MN=2,问MN在x轴上移动到何处时,四边形PQNM的周长最小?请直接写出符合条件的点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com