
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M从点C出发,以每秒1cm的速度沿CA向终点A移动,同时动点P从点A出发,以每秒2cm的速度沿AB向终点B移动,连接PM,设移动时间为t(s)(0<t<2.5).
(1)当AP=AM时,求t的值.
(2)设四边形BPMC的面积为 (cm²),求y与t之间的函数关系式;
(cm²),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形BPMC的面积是Rt△ABC面积的 ?若存在,求出相应t的值,若不存在,说明理由;
?若存在,求出相应t的值,若不存在,说明理由;
(4)是否存在某一时刻t,使以M,P,A为顶点的三角形与△ABC相似?若存在,求出相应t的值;若不存在,说明理由.
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
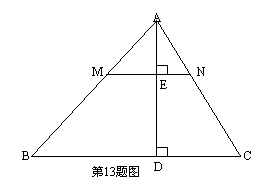
如图,AD是△ABC的高,点M在AB边上,点N在AC边上,MN⊥AD,垂足为E.下列说法正确的是 .(只填序号)
①若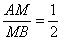 ,则
,则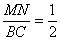 ;②
;②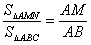 ;
;
③若△AMN与△ABC的相似比是2:3,且△AMN的周长为6,则△ABC的周长为9;
④若 ,则
,则 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°且距离A点20海里的C处救生船,此时,遇险船在救生船的正东方向B处,现救生船沿着航线CB前往B处救援,求救生船到达B处行驶的距离?(参考数据:sin68°≈0.90,cos68°≈0.36,tan68°≈2.50, ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
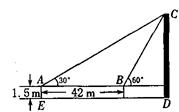
如图,为了测量某建筑物CD的高度,测量人员先在地面上用测角仪AE自A处测得建筑物顶部C的仰角是30°,然后在水平地面上向建筑物前进42 m,此时自B处测得建筑物顶部C的仰角是60°,已知测角仪的高度始终是1.5 m,则该建筑物CD的高度约为_______m(结果保留到1m,参考数 据:
据: ≈1.4,
≈1.4, ≈1.7).
≈1.7).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com