
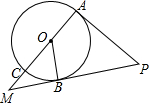
 如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.分析 (1)根据切线的性质,可得∠MAP=90°,根据直角三角形的性质,可得∠P+M=90°,根据余角的性质,可得∠M+∠MOB=90°,根据直角三角形的判定,可得∠MOB=90°,根据切线的判定,可得答案;
(2)根据相似三角形的判定与性质,可得$\frac{MB}{AM}$=$\frac{OB}{AP}$=$\frac{OM}{PB}$,根据解方程组,可得答案.
解答 (1)证明:∵PA切⊙O于点A,
∴∠MAP=90°,
∴∠P+∠M=90°.
∵∠COB=∠APB,
∴∠M+∠MOB=90°,
∴∠MBO=90°,即OB⊥PB,
∵PB经过直径的外端点,
∴PB是⊙O的切线;
(2)∵∠COB=∠APB,∠OBM=∠PAM,
∴△OBM∽△APM,
∴$\frac{MB}{AM}$=$\frac{OB}{AP}$=$\frac{OM}{PM}$,
$\frac{MB}{MC+6}$=$\frac{1}{2}$ ①,
$\frac{MC+3}{MB+6}$=$\frac{1}{2}$ ②
联立①②得$\left\{\begin{array}{l}{2MB=MC+6}\\{2MC+6=MB+6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{MC=2}\\{MB=4}\end{array}\right.$,
当OB=3,PA=6时,MB=4,MC=2.
点评 本题考查了切线的判定与性质,(1)利用了切线的判定与性质,直角三角形的判定与性质,余角的性质;(2)利用了相似三角形的判定与性质,解方程组.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
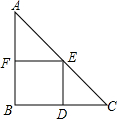 如图,在Rt△ABC中,AB=BC,∠B=90°,AC=10$\sqrt{2}$.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是25.
如图,在Rt△ABC中,AB=BC,∠B=90°,AC=10$\sqrt{2}$.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是25.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24cm | B. | 48cm | C. | 96cm | D. | 192cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
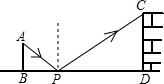 如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2米,BP=3米,PD=12米,那么该古城墙的高度CD是8米.
如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2米,BP=3米,PD=12米,那么该古城墙的高度CD是8米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com