
科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 14 | C. | 10或14 | D. | 8或10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6,3,1 | B. | 3,6,1 | C. | 2,1,3 | D. | 2,3,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
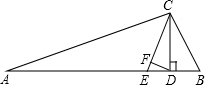 △ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.
△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com