
| 购进数量(件) | 购进所需费用(元) | ||
| A | B | ||
| 第一次 | 30 | 40 | 3800 |
| 第二次 | 40 | 30 | 3200 |
分析 (1)设A种商品每件的进价为x元,B种商品每件的进价为y元,根据两次进货情况表,可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购进B种商品m件,获得的利润为w元,则购进A种商品(1000-m)件,根据总利润=单件利润×购进数量,即可得出w与m之间的函数关系式,由A种商品的数量不少于B种商品数量的4倍,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,再根据一次函数的性质即可解决最值问题.
解答 解:(1)设A种商品每件的进价为x元,B种商品每件的进价为y元,
根据题意得:$\left\{\begin{array}{l}{30x+40y=3800}\\{40x+30y=3200}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=20}\\{y=80}\end{array}\right.$.
答:A种商品每件的进价为20元,B种商品每件的进价为80元.
(2)设购进B种商品m件,获得的利润为w元,则购进A种商品(1000-m)件,
根据题意得:w=(30-20)(1000-m)+(100-80)m=10m+10000.
∵A种商品的数量不少于B种商品数量的4倍,
∴1000-m≥4m,
解得:m≤200.
∵在w=10m+10000中,k=10>0,
∴w的值随m的增大而增大,
∴当m=200时,w取最大值,最大值为10×200+10000=12000,
∴当购进A种商品800件、B种商品200件时,销售利润最大,最大利润为12000元.
点评 本题考查了一次函数的应用、二元一次方程组的应用以及解一元一次不等式,解题的关键是:(1)找准等量关系,列出二元一次方程组;(2)根据数量关系,找出w与m之间的函数关系式.


科目:初中数学 来源: 题型:解答题
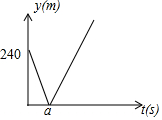 甲,乙两人沿同一条滨海大道同起点、同方向进行体育锻炼,已知甲匀速跑步,先出发60s,乙匀速骑车,速度是甲的两倍,在锻炼的过程中,设甲乙两人相距y(m),乙骑车的时间为t(s),y是t的函数,其图象的一部分如图所示.
甲,乙两人沿同一条滨海大道同起点、同方向进行体育锻炼,已知甲匀速跑步,先出发60s,乙匀速骑车,速度是甲的两倍,在锻炼的过程中,设甲乙两人相距y(m),乙骑车的时间为t(s),y是t的函数,其图象的一部分如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
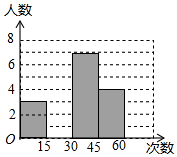 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:| 分 组 | 频数 | 频率 |
| 第一组(0≤x<15) | 3 | 0.15 |
| 第二组(15≤x<30) | a | 0.3 |
| 第三组(30≤x<45) | 7 | 0.35 |
| 第四组(45≤x<60) | 4 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 身高/cm | 159 | 160 | 161 | 162 |
| 人数 | 7 | 10 | 9 | 9 |
| A. | 160和160 | B. | 160和160.5 | C. | 160和161 | D. | 161和161 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
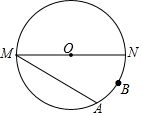 如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为$\widehat{AN}$的中点,P是直径MN上一动点.
如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为$\widehat{AN}$的中点,P是直径MN上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=3(x-1)2-1 | B. | y=3(x+1)2-1 | C. | y=3(x-1)2+1 | D. | y=3(x+1)2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.85×109 | B. | 1.85×1010 | C. | 1.85×1011 | D. | 1.85×1012 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com