
分析 根据根与系数的关系可得出x1+x2=$\frac{4}{3}$、x1•x2=$\frac{1}{3}$,将其代入$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$中即可求出结论.
解答 解:∵方程3x2-4x+1=0的两个根是x1、x2,
∴x1+x2=$\frac{4}{3}$,x1•x2=$\frac{1}{3}$,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{\frac{4}{3}}{\frac{1}{3}}$=4.
故答案为:4.
点评 本题考查了根与系数的关系,牢记两根之和等于-$\frac{b}{a}$、两根之积等于$\frac{c}{a}$是解题的关键.


科目:初中数学 来源: 题型:填空题
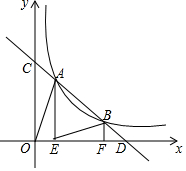 如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上(点A在点B的左侧),直线AB分别交x轴,y轴于点D,C,AE⊥x轴于点E,BF⊥x轴于点F,连结AO,BE,已知AB=2BD,△AOC与△BDF的面积之和是△ABE的面积的k倍,则k的值是$\frac{5}{6}$.
如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上(点A在点B的左侧),直线AB分别交x轴,y轴于点D,C,AE⊥x轴于点E,BF⊥x轴于点F,连结AO,BE,已知AB=2BD,△AOC与△BDF的面积之和是△ABE的面积的k倍,则k的值是$\frac{5}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.1415926 | B. | $\frac{22}{7}$ | C. | π | D. | $\sqrt{36}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在矩形ABCD中,DC=4$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.
在矩形ABCD中,DC=4$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
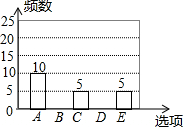 随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.玩游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如图表(部分信息未给出):
随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.玩游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如图表(部分信息未给出):| 选项 | 频数 | 百分比 |
| A | 10 | m |
| B | n | 0.2 |
| C | 5 | 0.1 |
| D | p | 0.4 |
| E | 5 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
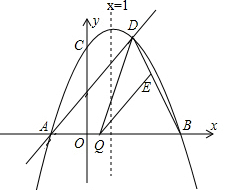 已知:如图,二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).
已知:如图,二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com